Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Queries to check if it is possible to join boxes in a circles in C++ Program
In this problem, we are given a number n that denotes n boxes that lie on the edge of a circle. And there are Q queries each consisting of two integers, a and b. Our task is to create a program to solve queries to check if it is possible to join boxes in a circles.
Problem Description − To solve each query, we need to check the possibility of connecting box a and box b by a rod in such a way that the intersection of boxes from the last query cannot be disturbed. We need to print possible or not possible based on the condition.
Let’s take an example to understand the problem,
Input
n = 6 Q = 3 Queries = {{1, 3}, {2, 5}, {4, 5}}Output
Possible Not possible Possible
Explanation
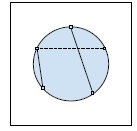
The solid lines are rods that can be connected, whereas the dashed line is the line that cannot be connected.
Solution Approach
A simple solution to the problem is by finding the solution of the query for each query, we will be finding whether the given boxes box a and box b can be connected. For this, we need to keep the values of the last query as reference points and then check if the connection is possible or not.
Let’s consider boxes a and b of the query (i-1) as reference ref1 and ref2. Then find if points a and b are at opposite sides of the rod.
For this, we will check for two conditions,
Condition 1 − if (ref1 < a < ref2 and ref2 < b < n)
Condition 2 − if (ref1 < b < ref2 and ref2 < a < n)
In both cases, the result will be not possible.
Here is the program to illustrate the working of our solution,
Example
#include <iostream>
using namespace std;
int printSolutoin(int n, int a, int b, int ref1, int ref2, int lastConn){
if(lastConn == 0 && a != b)
return 1;
int temp;
if(a > b){
temp = a;
a = b;
b = temp;
}
if(ref1 > ref2){
temp = ref1;
ref1 = ref2;
ref2 = temp;
}
if( ( ref1 < a && a < b && b < ref2) )
return 1;
if( (ref1 <= a <= ref2) && (ref2 <= b <= n) ) return 0;
else if( (ref1 <= b <= ref2) && (ref2 <= a <= n) )
return 0;
return 0;
return 1;
}
void solveAllQueries(int n, int q, int query[][2]){
int lastConn = printSolutoin(n, query[0][0], query[0][1], 0, 0, 0);
lastConn?cout<<"Possible\n":cout<<"Not Possible\n";
for(int i = 1; i < q; i++){
lastConn = printSolutoin(n, query[i][0], query[i][1], query[i - 1][0], query[0][1], lastConn);
lastConn?cout<<"Possible\n":cout<<"Not Possible\n";
}
}
int main() {
int n = 6;
int Q = 3;
int query[Q][2] = {{1, 3}, {2, 5}, {4, 5}};
return 0;
}Output
Possible Not Possible Possible
52 Views
