Prolog - Recursion in Family Relationship

In the previous section, we have seen that we can define some family relationships. These relationships are static in nature. We can also create some recursive relationships which can be expressed from the following illustration −

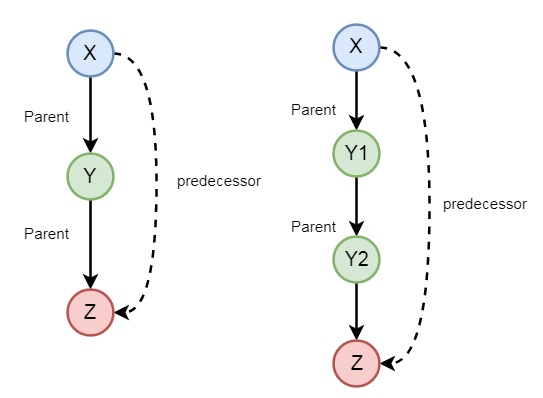
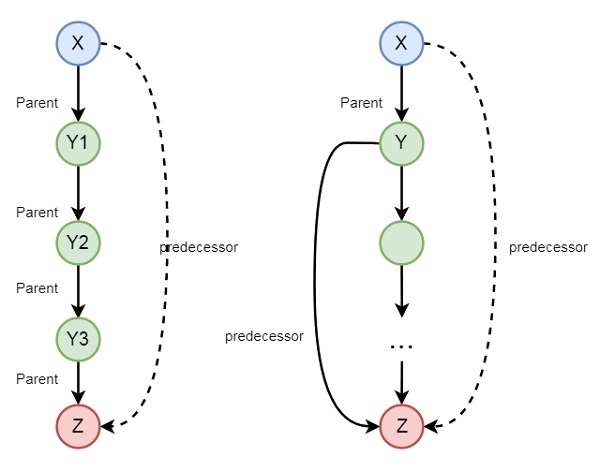
So we can understand that predecessor relationship is recursive. We can express this relationship using the following syntax −

predecessor(X, Z) :- parent(X, Z).
predecessor(X, Z) :- parent(X, Y),predecessor(Y, Z).

Now let us see the practical demonstration.

Knowledge Base (family_rec.pl)

female(pam).
female(liz).
female(pat).
female(ann).
male(jim).
male(bob).
male(tom).
male(peter).
parent(pam,bob).
parent(tom,bob).
parent(tom,liz).
parent(bob,ann).
parent(bob,pat).
parent(pat,jim).
parent(bob,peter).
parent(peter,jim).
predecessor(X, Z) :- parent(X, Z).
predecessor(X, Z) :- parent(X, Y),predecessor(Y, Z).

Output

| ?- consult('D:/TP Prolog/Sample Codes/family_rec.pl').
compiling D:/TP Prolog/Sample Codes/family_rec.pl for byte code...
D:/TP Prolog/Sample Codes/family_rec.pl compiled, 17 lines read - 1850 bytes written, 3 ms

(16 ms) yes
| ?- predecessor(peter,X).

X = jim ? ;

no
| ?- trace.
The debugger will first creep -- showing everything (trace)

yes
{trace}
| ?- predecessor(bob,X).
      1    1  Call: predecessor(bob,_23) ? 
      2    2  Call: parent(bob,_23) ? 
      2    2  Exit: parent(bob,ann) ? 
      1    1  Exit: predecessor(bob,ann) ? 

X = ann ? ;
      1    1  Redo: predecessor(bob,ann) ? 
      2    2  Redo: parent(bob,ann) ? 
      2    2  Exit: parent(bob,pat) ? 
      1    1  Exit: predecessor(bob,pat) ? 

X = pat ? ;
      1    1  Redo: predecessor(bob,pat) ? 
      2    2  Redo: parent(bob,pat) ? 
      2    2  Exit: parent(bob,peter) ? 
      1    1  Exit: predecessor(bob,peter) ? 

X = peter ? ;
      1    1  Redo: predecessor(bob,peter) ? 
      2    2  Call: parent(bob,_92) ? 
      2    2  Exit: parent(bob,ann) ? 
      3    2  Call: predecessor(ann,_23) ? 
      4    3  Call: parent(ann,_23) ? 
      4    3  Fail: parent(ann,_23) ? 
      4    3  Call: parent(ann,_141) ? 
      4    3  Fail: parent(ann,_129) ? 
      3    2  Fail: predecessor(ann,_23) ? 
      2    2  Redo: parent(bob,ann) ? 
      2    2  Exit: parent(bob,pat) ? 
      3    2  Call: predecessor(pat,_23) ? 
      4    3  Call: parent(pat,_23) ? 
      4    3  Exit: parent(pat,jim) ? 
      3    2  Exit: predecessor(pat,jim) ? 
      1    1  Exit: predecessor(bob,jim) ? 

X = jim ? ;
      1    1  Redo: predecessor(bob,jim) ? 
      3    2  Redo: predecessor(pat,jim) ? 
      4    3  Call: parent(pat,_141) ? 
      4    3  Exit: parent(pat,jim) ? 
      5    3  Call: predecessor(jim,_23) ? 
      6    4  Call: parent(jim,_23) ? 
      6    4  Fail: parent(jim,_23) ? 
      6    4  Call: parent(jim,_190) ? 
      6    4  Fail: parent(jim,_178) ? 
      5    3  Fail: predecessor(jim,_23) ? 
      3    2  Fail: predecessor(pat,_23) ? 
      2    2  Redo: parent(bob,pat) ? 
      2    2  Exit: parent(bob,peter) ? 
      3    2  Call: predecessor(peter,_23) ? 
      4    3  Call: parent(peter,_23) ? 
      4    3  Exit: parent(peter,jim) ? 
      3    2  Exit: predecessor(peter,jim) ? 
      1    1  Exit: predecessor(bob,jim) ? 

X = jim ? ;
      1    1  Redo: predecessor(bob,jim) ? 
      3    2  Redo: predecessor(peter,jim) ? 
      4    3  Call: parent(peter,_141) ? 
      4    3  Exit: parent(peter,jim) ? 
      5    3  Call: predecessor(jim,_23) ? 
      6    4  Call: parent(jim,_23) ? 
      6    4  Fail: parent(jim,_23) ? 
      6    4  Call: parent(jim,_190) ? 
      6    4  Fail: parent(jim,_178) ? 
      5    3  Fail: predecessor(jim,_23) ? 
      3    2  Fail: predecessor(peter,_23) ? 
      1    1  Fail: predecessor(bob,_23) ? 

(62 ms) no
{trace}
| ?- notrace.
The debugger is switched off

yes
| ?-