Prolog - Towers of Hanoi Problem

Towers of Hanoi Problem is a famous puzzle to move N disks from the source peg/tower to the target peg/tower using the intermediate peg as an auxiliary holding peg. There are two conditions that are to be followed while solving this problem −

• A larger disk cannot be placed on a smaller disk.

• Only one disk can be moved at a time.

The following diagram depicts the starting setup for N=3 disks.

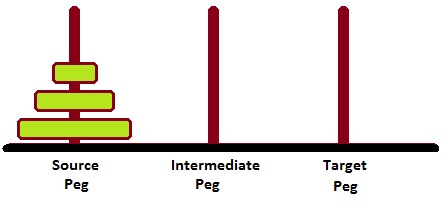
To solve this, we have to write one procedure move(N, Source, Target, auxiliary). Here N number of disks will have to be shifted from Source peg to Target peg keeping Auxiliary peg as intermediate.

For example move(3, source, target, auxiliary).

• Move top disk from source to target

• Move top disk from source to auxiliary

• Move top disk from target to auxiliary

• Move top disk from source to target

• Move top disk from auxiliary to source

• Move top disk from auxiliary to target

• Move top disk from source to target

Program(towersofhanoi.pl)

move(1,X,Y,_) :-   write('Move top disk from '), write(X), write(' to '), write(Y), nl.
move(N,X,Y,Z) :-   N>1,   M is N-1,   move(M,X,Z,Y),   move(1,X,Y,_),   move(M,Z,Y,X).

Output

| ?- consult('D:/TP Prolog/Sample Codes/towersofhanoi.pl').
compiling D:/TP Prolog/Sample Codes/towersofhanoi.pl for byte code...
D:/TP Prolog/Sample Codes/towersofhanoi.pl compiled, 1 lines read - 1409 bytes written, 3 ms

(16 ms) yes
| ?- move(4,source,target,auxiliary).
Move top disk from source to auxiliary
Move top disk from source to target
Move top disk from auxiliary to target
Move top disk from source to auxiliary
Move top disk from target to source
Move top disk from target to auxiliary
Move top disk from source to auxiliary
Move top disk from source to target
Move top disk from auxiliary to target
Move top disk from auxiliary to source
Move top disk from target to source
Move top disk from auxiliary to target
Move top disk from source to auxiliary
Move top disk from source to target
Move top disk from auxiliary to target

true ? 

yes
| ?-