Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to solve partially filled Sudoku Grid in C++
Suppose we have a partially filled Sudoku grid and we have to solve this. We know that Sudoku is a 9 × 9 number grid, and the whole grid are also divided into 3 × 3 boxes There are some rules to solve the Sudoku.
We have to use digits 1 to 9 for solving this problem.
One digit cannot be repeated in one row, one column or in one 3 × 3 box.
Using backtracking algorithm, we will try to solve Sudoku problem. When some cell is filled with a digit, it checks whether it is valid or not. When it is not valid, it checks for other numbers. If all numbers are checked from 1−9, and no valid digit found to place, it backtracks to previous option.
So if the input is like −
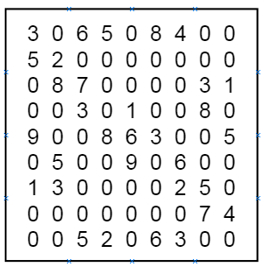
The output will be −
To solve this, we will follow these steps −
Define a method called isPresentInCol(), this will take call and num
for each row r in the grid, do
if grid[r, col] = num, then return true
return false otherwise
Define a method called isPresentInRow(), this will take row and num
for each column c in the grid, do
if grid[row, c] = num, then return true
return false otherwise
Define a method called isPresentInBox() this will take boxStartRow, boxStartCol, num
for each row r in boxStartRow to next 3 rows, do
for each col r in boxStartCol to next 3 columns, do
if grid[r, c] = num, then return true
return false otherwise
Define a method called findEmptyPlace(), this will take row and col
for each row r in the grid, do
for each column c in the grid, do
if grid[r, c] = 0, then return true
return false
Define a method called isValidPlace(), this will take row, col, num
if isPresentInRow(row, num) and isPresentInCol(col, num) and isPresntInBox(row − row mod 3, col − col mod 3, num) all are false, then return true
Define a method called solveSudoku(), this will take the grid
if no place in the grid is empty, then return true
for number 1 to 9, do
if isValidPlace(row, col, number), then
grid[row, col] := number
if solveSudoku = true, then return true
grid[row, col] := 0
return false
Let us see the following implementation to get better understanding −
Example
#include <iostream>
#define N 9
using namespace std;
int grid[N][N] = { {3, 0, 6, 5, 0, 8, 4, 0, 0},
{5, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 8, 7, 0, 0, 0, 0, 3, 1},
{0, 0, 3, 0, 1, 0, 0, 8, 0},
{9, 0, 0, 8, 6, 3, 0, 0, 5},
{0, 5, 0, 0, 9, 0, 6, 0, 0},
{1, 3, 0, 0, 0, 0, 2, 5, 0},
{0, 0, 0, 0, 0, 0, 0, 7, 4},
{0, 0, 5, 2, 0, 6, 3, 0, 0}};
bool isPresentInCol(int col, int num){
//check whether num is present
in col or not
for (int row = 0; row < N; row++)
if (grid[row][col] == num)
return true;
return false;
}
bool isPresentInRow(int row, int num){
//check whether num is present
in row or not
for (int col = 0; col < N; col++)
if (grid[row][col] == num)
return true;
return false;
}
bool isPresentInBox(int boxStartRow, int boxStartCol, int num){
//check whether num is present in 3x3 box or not
for (int row = 0; row < 3; row++)
for (int col = 0; col < 3; col++)
if (grid[row+boxStartRow][col+boxStartCol] == num)
return true;
return false;
}
void sudokuGrid(){
//print the sudoku grid after solve
for (int row = 0; row < N; row++){
for (int col = 0; col < N; col++){
if(col == 3 || col == 6)
cout << " | ";
cout << grid[row][col] <<" ";
}
if(row == 2 || row == 5){
cout << endl;
for(int i = 0; i<N; i++)
cout << "---";
}
cout << endl;
}
}
bool findEmptyPlace(int &row, int &col){
//get empty location and
update row and column
for (row = 0; row < N; row++)
for (col = 0; col < N; col++)
if (grid[row][col] == 0) //marked with 0 is empty
return true;
return false;
}
bool isValidPlace(int row, int col, int num){
//when item not found in col, row and current 3x3 box
return !isPresentInRow(row, num) && !isPresentInCol(col, num) &&
for (int row = 0; row < N; row++){
for (int col = 0; col < N; col++){
if(col == 3 || col == 6)
cout << " | ";
cout << grid[row][col] <<" ";
}
if(row == 2 || row == 5){
cout << endl;
for(int i = 0; i<N; i++)
cout << "−−−";
}
cout << endl;
}
}
bool findEmptyPlace(int &row, int &col){
//get empty location and
update row and column
for (row = 0; row < N; row++)
for (col = 0; col < N; col++)
if (grid[row][col] == 0) //marked with 0 is empty
return true;
return false;
}
bool isValidPlace(int row, int col, int num){
//when item not found in col, row and current 3x3 box
return !isPresentInRow(row, num) && !isPresentInCol(col, num) &&
cout << "No solution exists";
}Input
{3, 0, 6, 5, 0, 8, 4, 0, 0},
{5, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 8, 7, 0, 0, 0, 0, 3, 1},
{0, 0, 3, 0, 1, 0, 0, 8, 0},
{9, 0, 0, 8, 6, 3, 0, 0, 5},
{0, 5, 0, 0, 9, 0, 6, 0, 0},
{1, 3, 0, 0, 0, 0, 2, 5, 0},
{0, 0, 0, 0, 0, 0, 0, 7, 4},
{0, 0, 5, 2, 0, 6, 3, 0, 0}Output
3 1 6 | 5 7 8 | 4 9 2 5 2 9 | 1 3 4 | 7 6 8 4 8 7 | 6 2 9 | 5 3 1 --------------------------- 2 6 3 | 4 1 5 | 9 8 7 9 7 4 | 8 6 3 | 1 2 5 8 5 1 | 7 9 2 | 6 4 3 --------------------------- 1 3 8 | 9 4 7 | 2 5 6 6 9 2 | 3 5 1 | 8 7 4 7 4 5 | 2 8 6 | 3 1 9
205 Views
