Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to print pentatope numbers upto Nth term in C
Program Description
A pentatope number is a number in the fifth cell of any row of Pascal's triangle starting with the 5-term row 1 4 6 4 1 either from left to right or from right to left.
The first few numbers of this kind are
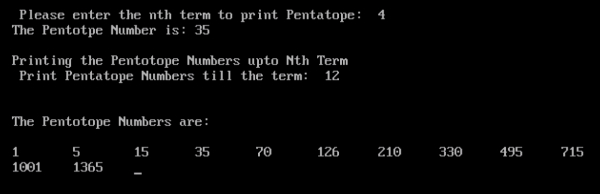
1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, 1365
Pentatope numbers belong in the class of figurate numbers, which can be represented as regular, discrete geometric patterns. The formula for the nth pentatopic number is
$$\left(\begin{array}{c}n+3\ 4\end{array}\right)=\left(\frac{n(n+1)+(n+2)+(n+3)}{24}\right)=\left(\frac{n^2}{4!}\right)$$
Algorithm
Accept the Nth Term from the User to find the Pentotope Numbers.
Use the formula
$$\left(\begin{array}{c}n+3\ 4\end{array}\right)=\left(\frac{n(n+1)+(n+2)+(n+3)}{24}\right)=\left(\frac{n^2}{4!}\right)$$
Example
/* Program to print pentatope numbers upto Nth term */
#include<stdio.h>
int main() {
int n, n1, nthterm, nthterm1, i;
clrscr();
printf("
Please enter the nth term to print Pentatope: ");
scanf("%d",&n);
nthterm = n * (n + 1) * (n + 2) * (n + 3) / 24;
printf("The Pentotpe Number is: ");
printf("%d", nthterm);
printf("
");
printf("Printing the Pentotope Numbers upto Nth Term");
printf("
Print Pentatope Numbers till the term: ");
scanf("%d",&n1);
printf("
");
printf("The Pentotope Numbers are:");
printf("
");
for (i = 1; i <= n1; i++){
nthterm1 = (i * (i + 1) * (i + 2) * (i + 3) / 24);
printf("%d\t", nthterm1);
}
getch();
return 0;
}Output
Updated on: 09-Jan-2020
157 Views
Advertisements