Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to count number of queries that are true in a graph with weighted path in C++
Suppose we have an edge list for an undirected graph where each edge has [u, v, w] fields, u and v are source and destination vertices and w is the weight. And also have a list of queries of the same form [u, v, w]. That represents the question of does there exist a path between u and v such that each edge in the path have weight of at most w. So find the number of queries that are true.
So, if the input is like edges = [[0, 1, 6],[1, 2, 7],[2, 3, 8],[0, 3, 5]] queries = [[0, 2, 14],[1, 0, 3]]
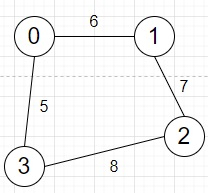
then the output will be 1, as we can go from node 0 to 2 by following this path [0, 1, 2] with weight 13. But there is no path from 1 to 0 with edge weight 3.
To solve this, we will follow these steps −
- Define a function get_parent(), this will take x, an array par,
- if par[x] is not x, then
- par[x] := get_parent(par[x], par)
- return par[x]
- From the main method do the following −
- Define one 2D array gr
- n := 0
- for each edge t in edges −
- n := maximum of n, t[0] and t[1]
- insert a row [t[2], 0, t[0], t[1]] into gr
- for each query t in queries −
- insert a row [t[2], 1, t[0], t[1]] into gr
- sort gr
- Define an array par of size n + 1 and fill with -1
- for initialize i := 0, when i <= n, update (increase i by 1), do −
- par[i] := i
- sz := size of queries
- ans := 0
- for each row t in gr
- a := t[2], b := t[3], tp := t[1], d := t[0]
- px := get_parent(a, par)
- py := get_parent(b, par)
- if tp is same as 0, then −
- if px is not equal to py, then −
- par[py] := px
- if px is not equal to py, then −
- Otherwise
- if px is same as py, then −
- (increase ans by 1)
- (decrease sz by 1)
- if sz is same as 0, then −
- Come out from the loop
- if px is same as py, then −
- return ans
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
int get_parent(int x, vector<int>& par) {
if (par[x] != x) {
par[x] = get_parent(par[x], par);
}
return par[x];
}
int solve(vector<vector<int>>& edges, vector<vector<int>>& queries) {
vector<vector<int>> gr;
int n = 0;
for (auto t : edges) {
n = max(n, max(t[0], t[1]));
gr.push_back({t[2], 0, t[0], t[1]});
}
for (auto t : queries) {
gr.push_back({t[2], 1, t[0], t[1]});
}
sort(gr.begin(), gr.end());
vector<int> par(n + 1, -1);
for (int i = 0; i <= n; i++) {
par[i] = i;
}
int sz = queries.size();
int ans = 0;
for (auto t : gr) {
int a = t[2];
int b = t[3];
int tp = t[1];
int d = t[0];
int px = get_parent(a, par);
int py = get_parent(b, par);
if (tp == 0) {
if (px != py) {
par[py] = px;
}
}else {
if (px == py) {
ans++;
}
sz--;
if(sz == 0) {
break;
}
}
}
return ans;
}
int main(){
vector<vector<int>> edges = {{0, 1, 6},{1, 2, 7},{2, 3, 8},{0, 3, 5}};
vector<vector<int>> queries = {{0, 2, 14},{1, 0, 3}};
cout << solve(edges, queries);
}Input
{{0, 1, 6},{1, 2, 7},{2, 3, 8},{0, 3, 5}}, {{0, 2, 14},{1, 0, 3}}Output
1
43 Views
