Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program for Point of Intersection of Two Lines in C++
Given points A and B corresponding to line AB and points P and Q corresponding to line PQ; the task is to find the point of intersection between these two lines.
Note − The points are given in 2D plane on X and Y coordinates.
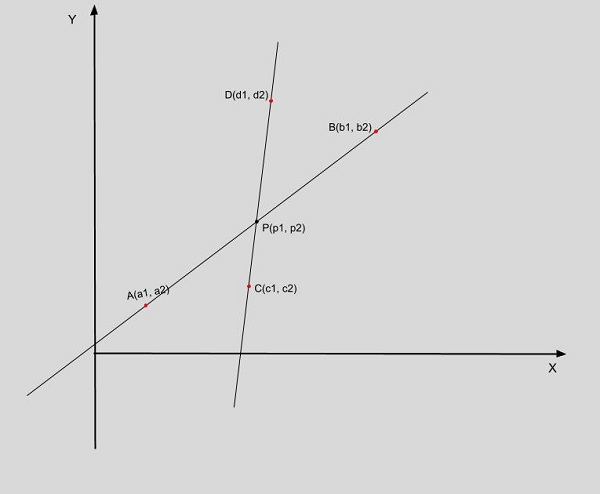
Here A(a1, a2), B(b1, b2) and C(c1, c2), D(d1, d2) are the coordinates which are forming two distinct lines and P(p1, p2) is the point of intersection. (just for diagrammatic explanation of point of intersection)
How to find the point of intersection −
Let’s take above figure as −
Example
So using the (a1, a2), (b1, b2), (c1, c2), (d1, d2) We will calculate : A1 = b2 - a2 B1 = a1 - b1 C1 = (A1 * a1) + (B1 * a1) A2 = d2 - c2 B2 = c1 - d1 C2 = (A2 * c1) + (B2 * c2) Let the given lines be: 1. A1x + B1y = C1 2. A2x + B2y = C2 Now, to find the point of intersection, we have to solve these 2 equations. We will multiply 1 by B1 and 2 by B2, so we will get: A1B2x +B1B2y = C1B2 A1B1x +B2B1y = C1B1 Subtracting these we get, (A1B2 - A2B1)x = C1B2-C2B1
This gives us value of x, and similarly we will get the value of y which will be the point of intersection p1 which is x and p2 which is y.
Note − the above formula will give the point of intersection of the two lines, but if the segments are given instead of lines, then we have to recheck that the point so the computed result must lie on the line segment.
- min (x1, x2) <= x <= max (x1, x2)
- min (y1, y2) <= y <= max (y1, y2)
Approach we are using to solve the above problem −
- Take the input values.
- Find the determinant which is a1 * b2 - a2 * b1
- Check if the determinant = 0 then the lines are parellel
- If the determinant is not zero then x = (c1 * b2 - c2 * b1) and y = (a1 * c2 - a2 * c1)
- Return and print the result.
Algorithm
Start Step 1-> Declare function to print the x and y coordinates void display(mk_pair par) Print par.first and par.second Step 2-> declare function to calculate the intersection point mk_pair intersection(mk_pair A, mk_pair B, mk_pair C, mk_pair D) Declare double a = B.second - A.second Declare double b = A.first - B.first Declare double c = a*(A.first) + b*(A.second) Declare double a1 = D.second - C.second Declare double b1 = C.first - D.first Declare double c1 = a1*(C.first)+ b1*(C.second) Declare double det = a*b1 - a1*b IF (det = 0) return make_pair(FLT_MAX, FLT_MAX) End Else Declare double x = (b1*c - b*c1)/det Declare double y = (a*c1 - a1*c)/det return make_pair(x, y) End Step 3-> In main() Declare and call function for points as mk_pair q = make_pair(2, 1) IF (inter.first = FLT_MAX AND inter.second = FLT_MAX) Print “given lines are parallel“ End Else Call display(inter) End Stop
Example
#include <bits/stdc++.h>
using namespace std;
#define mk_pair pair<double, double>
//display the x and y coordinates
void display(mk_pair par) {
cout << "(" << par.first << ", " << par.second << ")" << endl;
}
mk_pair intersection(mk_pair A, mk_pair B, mk_pair C, mk_pair D) {
// Line AB represented as a1x + b1y = c1
double a = B.second - A.second;
double b = A.first - B.first;
double c = a*(A.first) + b*(A.second);
// Line CD represented as a2x + b2y = c2
double a1 = D.second - C.second;
double b1 = C.first - D.first;
double c1 = a1*(C.first)+ b1*(C.second);
double det = a*b1 - a1*b;
if (det == 0) {
return make_pair(FLT_MAX, FLT_MAX);
} else {
double x = (b1*c - b*c1)/det;
double y = (a*c1 - a1*c)/det;
return make_pair(x, y);
}
}
int main() {
mk_pair q = make_pair(2, 1);
mk_pair r = make_pair(2, 7);
mk_pair s = make_pair(4, 4);
mk_pair t = make_pair(6, 4);
mk_pair inter = intersection(q, r, s, t);
if (inter.first == FLT_MAX && inter.second==FLT_MAX) {
cout << "The given lines AB and CD are parallel.\n";
} else {
cout << "The intersection of the given lines AB and CD is: ";
display(inter);
}
return 0;
}Output
The intersection of the given lines AB and CD is: (2, 4)
3K+ Views
