Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Product of middle row and column in an odd square matrix in C
Given a square matrix, mat[row][column] where row and column are equal and are of odd length means the number of row and column must me odd, i.e, not divisible by 2, the task is to find the product of middle row and middle column of that matrix.
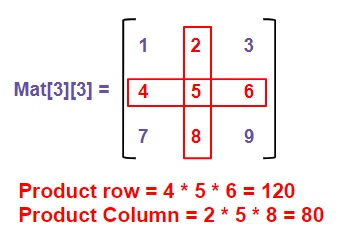
Like in the given figure below −
Constraints
Matrix must be a square matrix.
Column and rows must be of odd length.
Input
mat[][] = {{1, 2, 3},
{4, 5, 6},
{7, 8, 9}}Output
Product of middle row = 120 Product of middle column = 80
Explanation
Product of middle row = 4 * 5 * 6 = 120 Product of middle column = 2 * 5 * 8 = 80
Input
mat[][] = {{3, 5, 0},
{1, 2, 7},
{9, 0, 5}}Output
Product of middle row = 14 Product of middle column = 0
Explanation
Product of middle row = 1 * 2 * 7 = 120 Product of middle column = 5 * 2 * 0 = 0
Approach used below is as follows to solve the problem
Take a matrix mat[][] as an input.
Traverse the matrix as from the middle row and middle column
Calculate the product of the middle row and middle column and return the result.
Algorithm
Start
In function int product(int mat[][MAX], int n)
Step 1→ Declare and initialize rproduct = 1, cproduct = 1
Step 2→ Loop For i = 0 and i < n and i++
Set rproduct = rproduct * mat[n / 2][i]
Set cproduct = cproduct * mat[i][n / 2]
Step 3→ Print "Product of middle row: rproduct “
Step 4→ Print "Product of middle column: cproduct”
In function int main()
Step 1→ Declare and initialize mat[][MAX] {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } }
Step 2→ Call product(mat, MAX)
StopExample
#include <stdio.h>
#define MAX 3
int product(int mat[][MAX], int n){
int rproduct = 1, cproduct = 1;
//We will only check the middle elements and
//find their products
for (int i = 0; i < n; i++) {
rproduct *= mat[n / 2][i];
cproduct *= mat[i][n / 2];
}
// Printing the result
printf("Product of middle row: %d
", rproduct);
printf("Product of middle column: %d
", cproduct);
return 0;
}
// Driver code
int main(){
int mat[][MAX] = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
product(mat, MAX);
return 0;
}Output
If run the above code it will generate the following output −
Product of middle row: 120 Product of middle column: 80
Updated on: 13-Aug-2020
177 Views
Advertisements