Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Priority Queue Introduction in C/C++
A priority queue is a type of queue in which elements are inserted or deleted according to the priorities assigned to them where priority is an integer value that can range between 0-10 where 0 shows the element with the highest priority and 10 shows the element with the lowest priority. There are two rules that are followed for implementing priority queue −
- Data or element with the highest priority will get executed before the data or element with the lowest priority.
- If two elements have the same priority than they will be executed in the sequence they are added in the list.
There are multiple data structures available that can be used to implement priority queue like Stack, Queue and Linked List. In this article, we are explaining queue data structure. There are two ways that can used to implement the priority queue like −
- Maintain queue for multiple priorities in a single array
One way to implement priority queue is to maintain a queue for each priority. We can store these multiple queues in a single array where each queue will have two pointers i.e. Front and Rear. In queue, Front pointer is used to insert the element in a queue and it is incremented by 1 whenever the element is inserted and another pointer is rear which is used to delete or remove the element from the queue which is decremented by 1 whenever the element is removed from the queue. In the end, through the positions of the two pointers we can also determine the number of elements in the queue.
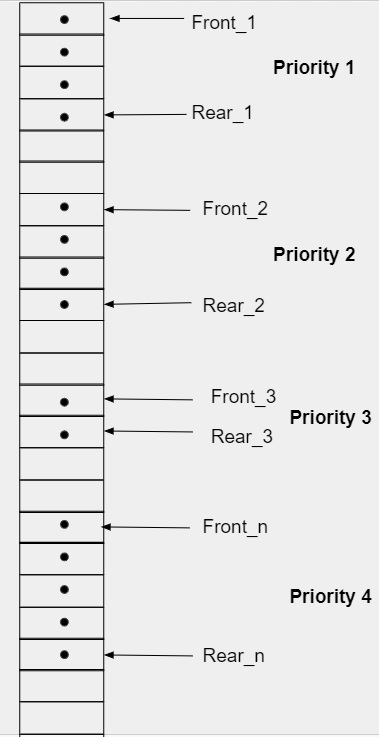
- In this type of representation, we need to shift the pointers to make space for inserting new elements which will make it complex in terms of time and space both.
- Maintain queue for each priority in a single array
In this type of method we create separate arrow for each element. Every queue is implemented as a circular array and have two pointer variables .i.e. Front and Rear. The element with give priority number is inserted in the corresponding queue likewise if we want to delete an element from the queue it must be the element from the highest priority queue. Lowest priority integer indicates the highest priority(0).
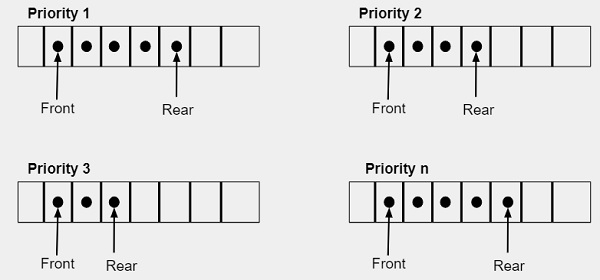
Note − If the size of each queue is same then we can create a single two dimensional array instead of creating multiple one-dimensional array.
Algorithm for Insert Operation In priority queue
insert(queue, data, priority) If(queue->Rear[priority] = MAX-1 AND queue->Front[priority] = 0) OR (queue->Rear[priority] +1 =queue->Front[priority]) Print Overflow End IF queue->Rear[priority - 1] = MAX-1 Set queue->Rear[priority - 1] = 0 Else Set queue->Rear[priority] = queue->Rear[priority - 1] +1 End Set queue->CQueue[priority - 1] [queue->Rear[priority - 1] = data IF queue->Front[priority - 1] = -1 Set queue->Front[priority - 1] = 0 End
Algorithm for Insert Operation In priority queue
delete(queue) Set flag = 0, priority = 0 While priority <= MAX-1 IF NOT queue->Front[priority] = -1 Set flag = 1 Set value = queue->CQueue[priority][queue->Front[priority]] IF queue->Front[priority] = queue->Rear[priority] Set queue->Front[priority] = queue->Rear[priority] = -1 Else IF queue->Front[priority] = MAX-1 Set queue->Front[priority] = 0 Else Set queue->Front[priority] = queue->Front[priority] + 1 End End Break End Set priority = priority + End If flag = 0 Print underflow Else Return value End
305 Views
