Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print numbers in matrix diagonal pattern in C Program.
The task is to print the matrix of n x n of the diagonal pattern.
If n is 3 then to print a matrix in Diagonal pattern is −
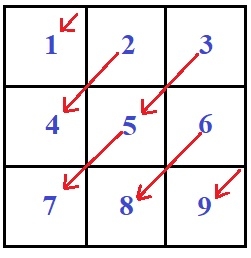
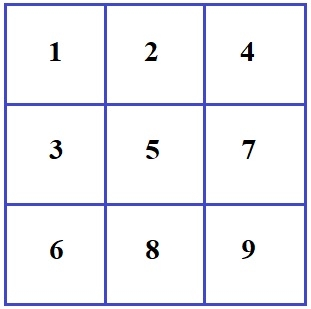
So the output will be like −
Example
Input: 3 Output: 1 2 4 3 5 7 6 8 9 Input: 4 Output: 1 2 4 7 3 5 8 11 6 9 12 14 10 13 15 16
The problem suggests we have to give a number n and generate a matrix of n x n and then we have to traverse the matrix in a diagonal pattern and store the values in a separate matrix.
But this will increase the complexity of our code, so we will −
Create a matrix of size N X N which will store the pattern before printing.
Store the elements in the upper triangle of the pattern. As observed the row index increases by 1 and the column index decreases by 1 as you move down the diagonal.
Once the upper triangle is completed then store the elements of the lower triangle in a similar way as the upper triangle i.e. row index increases by 1 and column index decreases by 1 as you move down the diagonal.
Algorithm
int printdiagonal(int n) START STEP 1: DECLARE int mat[n][n], i, j, k, d=1, m STEP 2: LOOP FOR i = 0 AND i < n AND i++ ASSIGN j AS i AND k AS 0 LOOP FOR j = I AND j >= 0 AND j-- ASSIGN mat[k][j] AS d INCREMENT d AND k BY 1 END LOOP END LOOP STEP 3: LOOP FOR k = 1 AND k < n AND k++ ASSIGN i AND m EQUALS TO k LOOP FOR j = n-1 AND j >= m AND j-- ASSIGN mat[i][j] AS d; INCREMENT d AND i WITH 1 END FOR END FOR STEP 4: LOOP FOR i = 0 AND i < n AND i++ LOOP FOR j = 0 AND j < n AND j++ PRINT mat[i][j] END FOR PRINT NEWLINE END FOR STOP
Example
#include <stdio.h>
int printdiagonal(int n){
int mat[n][n], i, j, k, d=1, m;
for ( i = 0; i < n; i++){
j = i;
k = 0;
for ( j = i; j >= 0; j--){
mat[k][j] = d;
d++;
k++;
}
}
for ( k = 1; k < n; k++){
i = m = k;
for ( j = n-1; j >= m; j--){
mat[i][j] = d;
d++;
i++;
}
}
for ( i = 0; i < n; i++){
for(j = 0; j < n; j++){
printf("%d ", mat[i][j] );
}
printf("
");
}
}
int main(int argc, char const *argv[]){
int n = 3;
printdiagonal(n);
return 0;
}Output
If we run the above program then it will generate the following output −
1 2 4 3 5 7 6 8 9
2K+ Views
