Print n x n spiral matrix using O(1) extra space in C Program.

We are given an positive integer n and make a spiral matrix of n x n, with only using O(1) extra space in clockwise direction

Spiral matrix is a matrix that works like a spiral which will start from the origin of a circle and rotates in clockwise fashion. So the task is to print the matrix in spiral form using O(1) space starting from 2 → 4 → 6 → 8 → 10 → 12 → 14 → 1 6→ 18.

Given below is the example of spiral matrix −

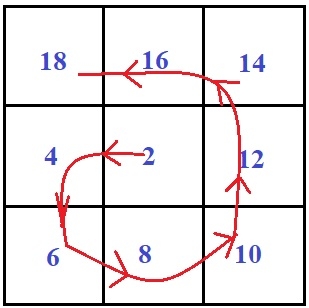
Example

Input: 3
Output:
   9 8 7
   2 1 6
   3 4 1

It becomes easy to solve the code with unlimited space but that is not efficient as best program or the code is the one which is efficient in memory and time both. So to maintain the spiral order four loops are used, each for top, right, bottom and left corner of the matrix but If we divide the matrix in two parts i.e. upper right and lower left we can directly use the concept

For upper right half,

mat[i][j] = (n-2*x)*(n-2*x)-(i-x)-(j-x)

For lower left half,

mat[i][j] = (n-2*x-2)*(n-2*x-2) + (i-x) + (j-x)

Note - We are writing program for printing the matrix multiple of 2

Algorithm

int spiralmatrix(int n)
START
STEP 1: DECLARE i, j, a, b, x
STEP 2: LOOP FOR i = 0 AND i < n AND i++
   LOOP FOR j = 0 AND j < n AND j++
      FIND THE MINIMUM IN (i<j ) AND ASSIGN IT TO a
      FIND THE MINIMUM (n-1-i) < (n-1-j) AND ASSIGN IT TO b
      THEN ASSIGN THE LEAST VALUE FROM a AND b TO x
      IF i <= j THEN,
         PRINT THE VALUE OF 2* ((n-2*x)*(n-2*x) - (i-x) - (j-x))
      ELSE
         PRINT THE VALUE OF 2*((n-2*x-2)*(n-2*x2) + (i-x) + (j-x))
   END LOOP
   PRINT NEWLINE
END LOOP
STOP

Example

#include <stdio.h>
//For n x n spiral matrix
int spiralmatrix(int n){
   int i, j, a, b, x; // x stores the layer in which (i, j)th element exist
   for ( i = 0; i < n; i++){
      for ( j = 0; j < n; j++){
         // Finds minimum of four inputs
         a = ((i<j ? i : j));
         b = ((n-1-i) < (n-1-j) ? (n-1-i) : (n-1-j));
         x = a < b ? a : b;
         // For upper right half
         if (i <= j)
            printf("%d\t ", 2 * ((n-2*x)*(n-2*x) - (i-x) - (j-x)));
            // for lower left half
         else
            printf("%d\t ", 2*((n-2*x-2)*(n-2*x-2) + (i-x) + (j-x)));
      }
      printf("
");
   }
}
int main(int argc, char const *argv[]){
   int n = 3;
   spiralmatrix(n);
   return 0;
}

Output

If we run above program then it will generate following output −

18 16 14
4 2 12
6 8 10