Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print N lines of numbers such that every pair among numbers has a GCD K
GCD
GCD stands for Greatest Common Divisor of two or more integers excluding 0
Like, to find the greatest common divisor of 48 and 180
48 = 2 × 2 × 2 × 2 × 3
180 = 2 × 2 × 3 × 3 × 5
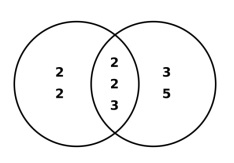
Greatest common divisor = 2 × 2 × 3 = 12.
In the given problem, N lines should be printed with elements have GCD as specified
Input : N=2 GCD=2 Ouput : 2-4-6-10 14-16-18-22
Algorithm
START Step 1 -> take input n(e.g. 2) and k(e.g. 2) as int values and i Step 2-> Loop For i to 0 and i<n and i++ Print (k * (6 * i + 1)) Print (k * (6 * i + 2)) Print (k * (6 * i +3)) Print (k * (6 * i + 5)) Print
Step 3 -> end loop STOP
Example
#include<stdio.h>
int main() {
int i,n = 2, k = 2;
for (i = 0; i < n; i++) {
printf("%d-",(k * (6 * i + 1)));
printf("%d-",(k * (6 * i + 2)));
printf("%d-",(k * (6 * i + 3)));
printf("%d",(k * (6 * i + 5)));
printf("
");
}
return 0;
}Output
if we run above program then it will generate following output.
2-4-6-10 14-16-18-22
Updated on: 30-Jul-2019
103 Views
Advertisements