Print all the levels with odd and even number of nodes in it in C++

In this problem, we are given a tree. And we have to print all the levels with even number of nodes and odd number of nodes in it.

Let’s take an example to understand the concept better

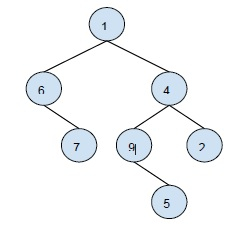
Output −

Levels with odd number of nodes: 1, 3, 4
Levels with even number of nodes: 2

Explanation − The first level has only 1 element(odd), 2nd level contains two elements(even), 3rd level contains 3 elements(odd) and 4th level contains 1 element(even).

Now, to solve this problem. We need to find the count of nodes at each level and print the even-odd levels accordingly.

We will follow the following steps to find the solution −

Step 1 − Run search algorithm for every level using height[node]=1+height[parent]

Step 2 − For every level store the number of nodes at that level.

Step 3 − iterate over the array containing elements, and print at even and odd levels.

Example

 Live Demo

#include <bits/stdc++.h>
using namespace std;
void traversal(int node, int parent, int height[], int vis[], vector<int> tree[]){
   height[node] = 1 + height[parent];
   vis[node] = 1;
   for (auto it : tree[node]) {
      if (!vis[it]) {
         traversal(it, node, height, vis, tree);
      }
   }
}
void insert(int x, int y, vector<int> tree[]){
   tree[x].push_back(y);
   tree[y].push_back(x);
}
void evenOddLevels(int N, int vis[], int height[]){
   int mark[N + 1];
   memset(mark, 0, sizeof mark);
   int maxLevel = 0;
   for (int i = 1; i <= N; i++) {
      if (vis[i])
         mark[height[i]]++;
      maxLevel = max(height[i], maxLevel);
   }
   cout << "The levels with odd number of nodes are: ";
   for (int i = 1; i <= maxLevel; i++) {
      if (mark[i] % 2)
         cout << i << " ";
   }
   cout << "\nThe levels with even number of nodes are: ";
   for (int i = 1; i <= maxLevel; i++) {
      if (mark[i] % 2 == 0)
         cout << i << " ";
   }
}
int main(){
   const int N = 9;
   vector<int> tree[N + 1];
   insert(1, 2, tree);
   insert(1, 3, tree);
   insert(2, 4, tree);
   insert(2, 5, tree);
   insert(5, 7, tree);
   insert(5, 8, tree);
   insert(3, 6, tree);
   insert(6, 9, tree);
   int height[N + 1];
   int vis[N + 1] = { 0 };
   height[0] = 0;
   traversal(1, 0, height, vis, tree);
   evenOddLevels(N, vis, height);
   return 0;
}

Output

The levels with odd number of nodes are: 1 3 4
The levels with even number of nodes are: 2