Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print all possible joints of a Trie constructed from a given list of string
In C++, the trie has an advanced data structure that is used for storing the collection of trees. The word tries came from the word retrieval and it is known as a digital tree or prefix tree.
Let’s take an example of all possible joint by taking a given list of strings.
We are defining the string input as {“tutor”, “true”, “tuo”}
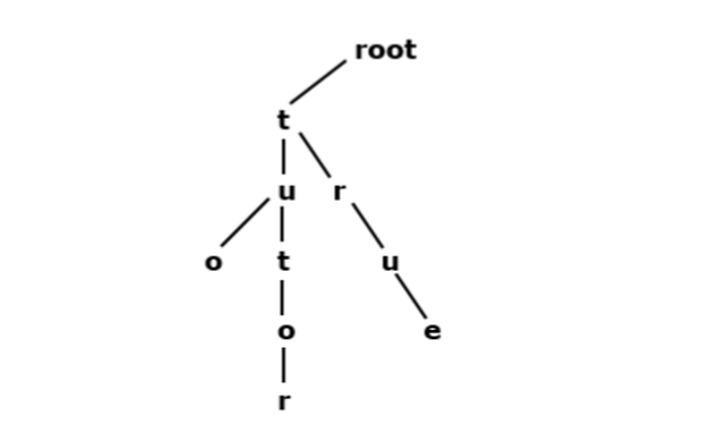
We can observe that the different string of characters is connected to the single string of the character. So here t and u are the list of characters in the string that joints all possible strings.
In this article, we are going to solve the list of a string having all the possible joints using a trie data structure.
Syntax
struct name_of_structure{
data_type var_name; // data member or field of the structure.
}
Parameters
struct − This keyword is used to represent structure datatype.
name_of_structure − We are providing any name to the structure.
The structure is a collection of various related variables in one place.
treetrie* alpha[alphabet]
The alpha is the name of the variable that points to the structure pointer/data member named treetrie. The alphabet is the macros that set the value of a total number of characters in integer form.
Algorithm
We start with a header file namely ‘bits/stdc++.h’ which includes all the standard template libraries of C++.
We are defining two macros namely ‘alphabet’ and ‘max’ that define the total character in an alphabet and the maximum of characters.
We are creating a structure name ‘tree node’ and define a pointer to ‘tree_node’ to store the address of alphabet. Defining the variable ‘end_word’ with bool data type which will be used for the ending character of a string.
We are defining a function name ‘buildNode’ using a pointer to connect a new node that represents the trie-constructed tree.
For inserting the string, we are creating a recursive function named ‘ins_recursive_of_string’ which accepts the three parameters- itm, str(the string to be inserted), i(indicating the current character being processed).
The function ins() is defined in the code as a wrapper function for ins_recursive_of_str(). It accepts two parameters: tree_trie* itm(a tree_trie object) and string str(a string to insert). It uses the current node, the string to be inserted, and the starting index 0 to call the recursive function.
Next, we are creating a function named is LeafNode() which takes a tree_trie object as an argument and checks if it is a leaf node, i.e. if it has no children.
The function display_joint() is defined in the code and takes four arguments: tree_trie* root, tree_trie*itm(the current node being processed), char str[](a character array str that stores the string formed by the path from the root node to the current node), and an int level(integer level that represents the depth of the current node).
The code defines the displayJ() function, which is a wrapper function for display_joint(). It takes a tree_trie object as an argument and calls the display_joint() function with the root node, an empty character array, and a starting level of 0 as arguments.
The code defines the main() function, which generates a new tree_trie object as Trie root node. It generates a vector s containing a list of strings to insert into the Trie. It then calls the ins() function to insert each string into the Trie.
Finally, it prints a message to indicate the beginning of the output and calls the displayJ() function to display all of the Trie joints.
Example
In this program, we are going to print all possible joints of trie constructed from a given list of strings.
#include <bits/stdc++.h>
using namespace std;
#define alphabet 26
#define max 200
// creating a structure for trie node
struct tree_trie {
tree_trie* alpha[alphabet];
bool end_word;
};
tree_trie* buildNode(){
tree_trie* temp = new tree_trie();
temp->end_word = false;
for (int i = 0; i < alphabet; i++) {
temp->alpha[i] = NULL;
}
return temp;
}
// We will insert the string using trie recursively
void ins_recursive_of_str(tree_trie* itm,
string str, int i){
if (i < str.length()) {
int idx = str[i] - 'a';
if (itm->alpha[idx] == NULL) {
// We are creating a new node
itm->alpha[idx] = buildNode();
}
// calling recursion function for inserting a string
ins_recursive_of_str(itm->alpha[idx],
str, i + 1);
}
else {
// We make the end_word true which represents the end of string
itm->end_word = true;
}
}
// By using function call we are inserting a tree
void ins(tree_trie* itm, string str){
// The necessary argument required for function call
ins_recursive_of_str(itm, str, 0);
}
// Using function we check whether the node is a leaf or not
bool isLeafNode(tree_trie* root){
return root->end_word != false;
}
// This function is an important part of the program to display the joints of trie
void display_joint(tree_trie* root, tree_trie* itm,
char str[], int level){
//Using this variable we are counting the current child
int current_alpha = 0;
for (int i = 0; i < alphabet; i++){
if (itm->alpha[i]) {
str[level] = i + 'a';
display_joint(root, itm->alpha[i],
str, level + 1);
current_alpha++;
}
}
// We are printing the character if it has more than 1 character
if (current_alpha > 1 && itm != root) {
cout << str[level - 1] << endl;
}
}
// By using this function call we are diplaying the joint of trie.
void displayJ(tree_trie* root){
int level = 0;
char str[max];
display_joint(root, root, str, level);
}
// main function
int main(){
tree_trie* root = buildNode();
vector<string> s = { "tutor", "true", "tuo"};
for (string str : s) {
ins(root, str);
}
cout<<"All possible joint of trie using the given list of string"<<endl;
displayJ(root);
return 0;
}
Output
All possible joint of trie using the given list of string u t
Conclusion
We explored the concept of trie data structure where we constructed all possible joints of trie from a given list of strings. We saw in the output how the characters u and t are connecting all possible joints of a trie by taking strings such as tutor, true, and tuo. So this way a tree can reduce its node by giving possible joints.
149 Views
