
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Prim’s (Minimum Spanning Tree) MST Algorithm
There is a connected graph G(V,E) and the weight or cost for every edge is given. Prim’s Algorithm will find the minimum spanning tree from the graph G.
It is growing tree approach. This algorithm needs a seed value to start the tree. The seed vertex is grown to form the whole tree.
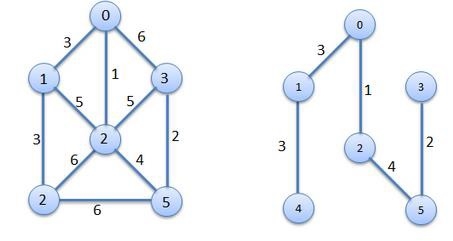
The problem will be solved using two sets. One set holds the nodes that are already selected, and another set holds the item that are not considered yet. From the seed vertex, it takes adjacent vertices, based on minimum edge cost, thus it grows the tree by taking nodes one by one.
Time complexity of this problem is O(V2). Here V is the number of vertices.
Input − The adjacency list −
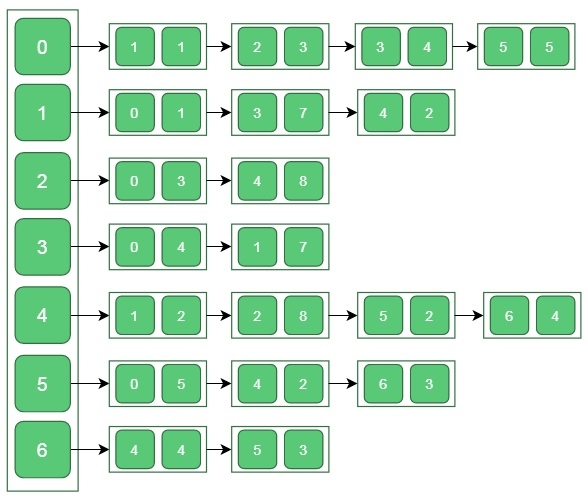
Output −
(0)---(1|1) (0)---(2|3) (0)---(3|4) (1)---(0|1) (1)---(4|2) (2)---(0|3) (3)---(0|4) (4)---(1|2) (4)---(5|2) (5)---(4|2) (5)---(6|3) (6)---(5|3)
Algorithm
prims(g: Graph, t: tree, start)
Input − The graph g, A blank tree and the seed vertex named ‘start’ Output: The Tree after adding edges.
Begin define two sets as usedVert, unusedVert usedVert[0] := start and unusedVert[0] := φ for all vertices except start do usedVert[i] := φ unusedVert[i] := i //add all vertices in unused list done while number of vertices in usedVert ≠ V do //V is number of total nodes min := ∞ for all vertices of usedVert array do for all vertices of the graph do if min > cost[i,j] AND i ≠ j then min := cost[i,j] ed := edge between i and j, and cost of ed := min done done unusedVert[destination of ed] := φ add edge ed into the tree t add source of ed into usedVert done End
Example(C++)
#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
{0, 1, 3, 4, INF, 5, INF},
{1, 0, INF, 7, 2, INF, INF},
{3, INF, 0, INF, 8, INF, INF},
{4, 7, INF, 0, INF, INF, INF},
{INF, 2, 8, INF, 0, 2, 4},
{5, INF, INF, INF, 2, 0, 3},
{INF, INF, INF, INF, 4, 3, 0}
};
typedef struct{
int u, v, cost;
}edge;
class Tree{
int n;
edge edges[V-1]; //as a tree has vertex-1 edges
public:
Tree(){
n = 0;
}
void addEdge(edge e){
edges[n] = e; //add edge e into the tree
n++;
}
void printEdges(){ //print edge, cost and total cost
int tCost = 0;
for(int i = 0; i<n; i++){
cout << "Edge: " << char(edges[i].u+'A') < "--" << char(edges[i].v+'A');
cout << " And Cost: " << edges[i].cost << endl;
tCost += edges[i].cost;
}
cout << "Total Cost: " << tCost << endl;
}
friend void prims(Tree &tre, int start);
};
void prims(Tree &tr, int start){
int usedVert[V], unusedVert[V];
int i, j, min, p;
edge ed;
//initialize
usedVert[0] = start; p = 1;
unusedVert[0] = -1;//-1 indicates the place is empty
for(i = 1; i<V; i++){
usedVert[i] = -1;//all places except first is empty
unusedVert[i] = i;//fill with vertices
}
tr.n = 0;
//get edges and add to tree
while(p != V){ //p is number of vertices in usedVert array
min = INF;
for(i = 0; i<p; i++){
for(j = 0; j<V; j++){
if(unusedVert[j] != -1){
if(min > costMat[i][j] && costMat[i][j] != 0){
//find the edge with minimum cost
//such that u is considered and v is not considered yet
min = costMat[i][j];
ed.u = i; ed.v = j; ed.cost = min;
}
}
}
}
unusedVert[ed.v] = -1;//delete v from unusedVertex
tr.addEdge(ed);
usedVert[p] = ed.u; p++;//add u to usedVertex
}
}
main(){
Tree tr;
prims(tr, 0); //starting node 0
tr.printEdges();
}
Output
(0)---(1|1) (0)---(2|3) (0)---(3|4) (1)---(0|1) (1)---(4|2) (2)---(0|3) (3)---(0|4) (4)---(1|2) (4)---(5|2) (5)---(4|2) (5)---(6|3) (6)---(5|3)

