Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Plain Rheostatic Starting of Traction Motors
In the plain rheostatic starting method, the voltage across the traction motor is gradually increased from zero to full line voltage and the current is kept constant at normal rated value by reducing the external resistance gradually.
Let,
𝑇 = Starting period in seconds
𝑉 = Line voltage in volts
𝐼 = Constant current in amperes
Then, at the instant of switching ON the supply, the back EMF produced by the motor is zero and it starts building up immediately as the motor starts rotating.
At any instant, the supply voltage to the motor is equal to the back EMF developed by the motor plus voltage drop in the series field and the armature of the motor plus voltage drop in the starting rheostat, i.e.,
$$\mathrm{\mathit{V\mathrm{\: =\: }E_{b}\mathrm{\: +\: }I\left ( R_{se} \mathrm{\: +\: }R_{a}\right )\mathrm{\: +\: }IR\mathrm{\: =\: }E_{b}\mathrm{\: +\: }IR_{m}\mathrm{\: +\: }IR}}$$
The following figure illustrates the voltage-drop and energy loss in the plain rheostatic starting of traction motors.
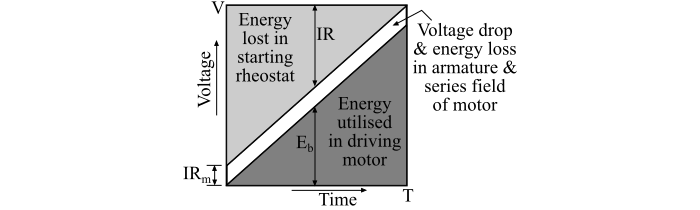
At the end of the starting period, external resistance is reduced to zero, and hence the voltage drop in the external resistance is zero and the back EMF becomes approximately equal to the line voltage, thus,
$$\mathrm{\mathit{E_{b}\mathrm{\: =\: }V-IR_{m}}}$$
Therefore, the energy drawn from the supply during starting is,
$$\mathrm{Energy\: during\: starting\mathrm{\: =\: }\mathit{V\times I\times T}}$$
The energy lost in the external resistance is,
$$\mathrm{Energy\: loss\: in\: external\: resistor\mathrm{\: =\: }Average\: voltage\: drop\: across\: the\: external \: resistance\times Current\times Time}$$
$$\mathrm{\Rightarrow Energy\: loss\: in\: external\: resistor\mathrm{\: =\: }\mathit{\frac{V-IR_{m}\mathrm{\: +\: }\mathrm{0}}{\mathrm{2}}\times I\times T}}$$
If voltage drop in series field and the armature of the motor is neglected, then,
$$\mathrm{\therefore Energy\: loss\: in\: external\: resistor\mathrm{\: =\: }\frac{1}{2}\mathit{V\times I\times T}}$$
Hence, the energy utilized in driving the motor is,
$$\mathrm{Energy \: utilised\mathrm{\: =\: }Energy\: supplied\, -\, Energy\: lost\: in\: external\: resistance}$$
$$\mathrm{\Rightarrow Energy \: utilised\mathrm{\: =\: }\mathit{VIT-\mathrm{\frac{1}{2}}VIT\mathrm{\: =\: }\mathrm{\frac{1}{2}}VIT}}$$
Also, the starting efficiency of the motor is,
$$\mathrm{\eta \mathrm{\: =\: }\frac{Energy\: utilised}{Energy\: Drawn}\times 100\mathrm{\: =\: }\mathit{\frac{VIT/\mathrm{2}}{VIT}}\times 100\mathrm{\: =\: }50\%}$$
473 Views
