
- Perl - Home
- Perl - Introduction
- Perl - Environment
- Perl - Syntax Overview
- Perl - Data Types
- Perl - Variables
- Perl - Scalars
- Perl - Arrays
- Perl - Hashes
- Perl - IF...ELSE
- Perl - Loops
- Perl - Operators
- Perl - Date & Time
- Perl - Subroutines
- Perl - References
- Perl - Formats
- Perl - File I/O
- Perl - Directories
- Perl - Error Handling
- Perl - Special Variables
- Perl - Coding Standard
- Perl - Regular Expressions
- Perl - Sending Email
- Perl - Socket Programming
- Perl - Object Oriented
- Perl - Database Access
- Perl - CGI Programming
- Perl - Packages & Modules
- Perl - Process Management
- Perl - Embedded Documentation
- Perl - Functions References
- Perl Useful Resources
- Perl - Questions and Answers
- Perl - Quick Guide
- Perl - Cheatsheet
- Perl - Useful Resources
- Perl - Discussion
Perl - Database Access
This chapter teaches you how to access a database inside your Perl script. Starting from Perl 5 has become very easy to write database applications using DBI module. DBI stands for Database Independent Interface for Perl, which means DBI provides an abstraction layer between the Perl code and the underlying database, allowing you to switch database implementations really easily.
The DBI is a database access module for the Perl programming language. It provides a set of methods, variables, and conventions that provide a consistent database interface, independent of the actual database being used.
Architecture of a DBI Application
DBI is independent of any database available in backend. You can use DBI whether you are working with Oracle, MySQL or Informix, etc. This is clear from the following architure diagram.
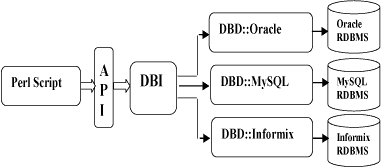
Here DBI is responsible of taking all SQL commands through the API, (i.e., Application Programming Interface) and to dispatch them to the appropriate driver for actual execution. And finally, DBI is responsible of taking results from the driver and giving back it to the calling scritp.
Notation and Conventions
Throughout this chapter following notations will be used and it is recommended that you should also follow the same convention.
$dsn Database source name $dbh Database handle object $sth Statement handle object $h Any of the handle types above ($dbh, $sth, or $drh) $rc General Return Code (boolean: true=ok, false=error) $rv General Return Value (typically an integer) @ary List of values returned from the database. $rows Number of rows processed (if available, else -1) $fh A filehandle undef NULL values are represented by undefined values in Perl \%attr Reference to a hash of attribute values passed to methods
Database Connection
Assuming we are going to work with MySQL database. Before connecting to a database make sure of the followings. You can take help of our MySQL tutorial in case you are not aware about how to create database and tables in MySQL database.
You have created a database with a name TESTDB.
You have created a table with a name TEST_TABLE in TESTDB.
This table is having fields FIRST_NAME, LAST_NAME, AGE, SEX and INCOME.
User ID "testuser" and password "test123" are set to access TESTDB.
Perl Module DBI is installed properly on your machine.
You have gone through MySQL tutorial to understand MySQL Basics.
Following is the example of connecting with MySQL database "TESTDB" −
#!/usr/bin/perl use DBI use strict; my $driver = "mysql"; my $database = "TESTDB"; my $dsn = "DBI:$driver:database=$database"; my $userid = "testuser"; my $password = "test123"; my $dbh = DBI->connect($dsn, $userid, $password ) or die $DBI::errstr;
If a connection is established with the datasource then a Database Handle is returned and saved into $dbh for further use otherwise $dbh is set to undef value and $DBI::errstr returns an error string.
INSERT Operation
INSERT operation is required when you want to create some records into a table. Here we are using table TEST_TABLE to create our records. So once our database connection is established, we are ready to create records into TEST_TABLE. Following is the procedure to create single record into TEST_TABLE. You can create as many as records you like using the same concept.
Record creation takes the following steps −
Preparing SQL statement with INSERT statement. This will be done using prepare() API.
Executing SQL query to select all the results from the database. This will be done using execute() API.
Releasing Stattement handle. This will be done using finish() API.
If everything goes fine then commit this operation otherwise you can rollback complete transaction. Commit and Rollback are explained in next sections.
my $sth = $dbh->prepare("INSERT INTO TEST_TABLE
(FIRST_NAME, LAST_NAME, SEX, AGE, INCOME )
values
('john', 'poul', 'M', 30, 13000)");
$sth->execute() or die $DBI::errstr;
$sth->finish();
$dbh->commit or die $DBI::errstr;
Using Bind Values
There may be a case when values to be entered is not given in advance. So you can use bind variables which will take the required values at run time. Perl DBI modules make use of a question mark in place of actual value and then actual values are passed through execute() API at the run time. Following is the example −
my $first_name = "john";
my $last_name = "poul";
my $sex = "M";
my $income = 13000;
my $age = 30;
my $sth = $dbh->prepare("INSERT INTO TEST_TABLE
(FIRST_NAME, LAST_NAME, SEX, AGE, INCOME )
values
(?,?,?,?)");
$sth->execute($first_name,$last_name,$sex, $age, $income)
or die $DBI::errstr;
$sth->finish();
$dbh->commit or die $DBI::errstr;
READ Operation
READ Operation on any databasse means to fetch some useful information from the database, i.e., one or more records from one or more tables. So once our database connection is established, we are ready to make a query into this database. Following is the procedure to query all the records having AGE greater than 20. This will take four steps −
Preparing SQL SELECT query based on required conditions. This will be done using prepare() API.
Executing SQL query to select all the results from the database. This will be done using execute() API.
Fetching all the results one by one and printing those results.This will be done using fetchrow_array() API.
Releasing Stattement handle. This will be done using finish() API.
my $sth = $dbh->prepare("SELECT FIRST_NAME, LAST_NAME
FROM TEST_TABLE
WHERE AGE > 20");
$sth->execute() or die $DBI::errstr;
print "Number of rows found :" + $sth->rows;
while (my @row = $sth->fetchrow_array()) {
my ($first_name, $last_name ) = @row;
print "First Name = $first_name, Last Name = $last_name\n";
}
$sth->finish();
Using Bind Values
There may be a case when condition is not given in advance. So you can use bind variables, which will take the required values at run time. Perl DBI modules makes use of a question mark in place of actual value and then the actual values are passed through execute() API at the run time. Following is the example −
$age = 20;
my $sth = $dbh->prepare("SELECT FIRST_NAME, LAST_NAME
FROM TEST_TABLE
WHERE AGE > ?");
$sth->execute( $age ) or die $DBI::errstr;
print "Number of rows found :" + $sth->rows;
while (my @row = $sth->fetchrow_array()) {
my ($first_name, $last_name ) = @row;
print "First Name = $first_name, Last Name = $last_name\n";
}
$sth->finish();
UPDATE Operation
UPDATE Operation on any database means to update one or more records already available in the database tables. Following is the procedure to update all the records having SEX as 'M'. Here we will increase AGE of all the males by one year. This will take three steps −
Preparing SQL query based on required conditions. This will be done using prepare() API.
Executing SQL query to select all the results from the database. This will be done using execute() API.
Releasing Stattement handle. This will be done using finish() API.
If everything goes fine then commit this operation otherwise you can rollback complete transaction. See next section for commit and rollback APIs.
my $sth = $dbh->prepare("UPDATE TEST_TABLE
SET AGE = AGE + 1
WHERE SEX = 'M'");
$sth->execute() or die $DBI::errstr;
print "Number of rows updated :" + $sth->rows;
$sth->finish();
$dbh->commit or die $DBI::errstr;
Using Bind Values
There may be a case when condition is not given in advance. So you can use bind variables, which will take required values at run time. Perl DBI modules make use of a question mark in place of actual value and then the actual values are passed through execute() API at the run time. Following is the example −
$sex = 'M';
my $sth = $dbh->prepare("UPDATE TEST_TABLE
SET AGE = AGE + 1
WHERE SEX = ?");
$sth->execute('$sex') or die $DBI::errstr;
print "Number of rows updated :" + $sth->rows;
$sth->finish();
$dbh->commit or die $DBI::errstr;
In some case you would like to set a value, which is not given in advance so you can use binding value as follows. In this example income of all males will be set to 10000.
$sex = 'M';
$income = 10000;
my $sth = $dbh->prepare("UPDATE TEST_TABLE
SET INCOME = ?
WHERE SEX = ?");
$sth->execute( $income, '$sex') or die $DBI::errstr;
print "Number of rows updated :" + $sth->rows;
$sth->finish();
DELETE Operation
DELETE operation is required when you want to delete some records from your database. Following is the procedure to delete all the records from TEST_TABLE where AGE is equal to 30. This operation will take the following steps.
Preparing SQL query based on required conditions. This will be done using prepare() API.
Executing SQL query to delete required records from the database. This will be done using execute() API.
Releasing Stattement handle. This will be done using finish() API.
If everything goes fine then commit this operation otherwise you can rollback complete transaction.
$age = 30;
my $sth = $dbh->prepare("DELETE FROM TEST_TABLE
WHERE AGE = ?");
$sth->execute( $age ) or die $DBI::errstr;
print "Number of rows deleted :" + $sth->rows;
$sth->finish();
$dbh->commit or die $DBI::errstr;
Using do Statement
If you're doing an UPDATE, INSERT, or DELETE there is no data that comes back from the database, so there is a short cut to perform this operation. You can use do statement to execute any of the command as follows.
$dbh->do('DELETE FROM TEST_TABLE WHERE age =30');
do returns a true value if it succeeded, and a false value if it failed. Actually, if it succeeds it returns the number of affected rows. In the example it would return the number of rows that were actually deleted.
COMMIT Operation
Commit is the operation which gives a green signal to database to finalize the changes and after this operation no change can be reverted to its orignal position.
Here is a simple example to call commit API.
$dbh->commit or die $dbh->errstr;
ROLLBACK Operation
If you are not satisfied with all the changes or you encounter an error in between of any operation , you can revert those changes to use rollback API.
Here is a simple example to call rollback API.
$dbh->rollback or die $dbh->errstr;
Begin Transaction
Many databases support transactions. This means that you can make a whole bunch of queries which would modify the databases, but none of the changes are actually made. Then at the end, you issue the special SQL query COMMIT, and all the changes are made simultaneously. Alternatively, you can issue the query ROLLBACK, in which case all the changes are thrown away and database remains unchanged.
Perl DBI module provided begin_work API, which enables transactions (by turning AutoCommit off) until the next call to commit or rollback. After the next commit or rollback, AutoCommit will automatically be turned on again.
$rc = $dbh->begin_work or die $dbh->errstr;
AutoCommit Option
If your transactions are simple, you can save yourself the trouble of having to issue a lot of commits. When you make the connect call, you can specify an AutoCommit option which will perform an automatic commit operation after every successful query. Here's what it looks like −
my $dbh = DBI->connect($dsn, $userid, $password,
{AutoCommit => 1})
or die $DBI::errstr;
Here AutoCommit can take value 1 or 0, where 1 means AutoCommit is on and 0 means AutoCommit is off.
Automatic Error Handling
When you make the connect call, you can specify a RaiseErrors option that handles errors for you automatically. When an error occurs, DBI will abort your program instead of returning a failure code. If all you want is to abort the program on an error, this can be convenient. Here's what it looks like −
my $dbh = DBI->connect($dsn, $userid, $password,
{RaiseError => 1})
or die $DBI::errstr;
Here RaiseError can take value 1 or 0.
Disconnecting Database
To disconnect Database connection, use disconnect API as follows −
$rc = $dbh->disconnect or warn $dbh->errstr;
The transaction behaviour of the disconnect method is, sadly, undefined. Some database systems (such as Oracle and Ingres) will automatically commit any outstanding changes, but others (such as Informix) will rollback any outstanding changes. Applications not using AutoCommit should explicitly call commit or rollback before calling disconnect.
Using NULL Values
Undefined values, or undef, are used to indicate NULL values. You can insert and update columns with a NULL value as you would a non-NULL value. These examples insert and update the column age with a NULL value −
$sth = $dbh->prepare(qq {
INSERT INTO TEST_TABLE (FIRST_NAME, AGE) VALUES (?, ?)
});
$sth->execute("Joe", undef);
Here qq{} is used to return a quoted string to prepare API. However, care must be taken when trying to use NULL values in a WHERE clause. Consider −
SELECT FIRST_NAME FROM TEST_TABLE WHERE age = ?
Binding an undef (NULL) to the placeholder will not select rows, which have a NULL age! At least for database engines that conform to the SQL standard. Refer to the SQL manual for your database engine or any SQL book for the reasons for this. To explicitly select NULLs you have to say "WHERE age IS NULL".
A common issue is to have a code fragment handle a value that could be either defined or undef (non-NULL or NULL) at runtime. A simple technique is to prepare the appropriate statement as needed, and substitute the placeholder for non-NULL cases −
$sql_clause = defined $age? "age = ?" : "age IS NULL";
$sth = $dbh->prepare(qq {
SELECT FIRST_NAME FROM TEST_TABLE WHERE $sql_clause
});
$sth->execute(defined $age ? $age : ());
Some Other DBI Functions
available_drivers
@ary = DBI->available_drivers; @ary = DBI->available_drivers($quiet);
Returns a list of all available drivers by searching for DBD::* modules through the directories in @INC. By default, a warning is given if some drivers are hidden by others of the same name in earlier directories. Passing a true value for $quiet will inhibit the warning.
installed_drivers
%drivers = DBI->installed_drivers();
Returns a list of driver name and driver handle pairs for all drivers 'installed' (loaded) into the current process. The driver name does not include the 'DBD::' prefix.
data_sources
@ary = DBI->data_sources($driver);
Returns a list of data sources (databases) available via the named driver. If $driver is empty or undef, then the value of the DBI_DRIVER environment variable is used.
quote
$sql = $dbh->quote($value); $sql = $dbh->quote($value, $data_type);
Quote a string literal for use as a literal value in an SQL statement, by escaping any special characters (such as quotation marks) contained within the string and adding the required type of outer quotation marks.
$sql = sprintf "SELECT foo FROM bar WHERE baz = %s",
$dbh->quote("Don't");
For most database types, quote would return 'Don''t' (including the outer quotation marks). It is valid for the quote() method to return an SQL expression that evaluates to the desired string. For example −
$quoted = $dbh->quote("one\ntwo\0three")
may produce results which will be equivalent to
CONCAT('one', CHAR(12), 'two', CHAR(0), 'three')
Methods Common to All Handles
err
$rv = $h->err; or $rv = $DBI::err or $rv = $h->err
Returns the native database engine error code from the last driver method called. The code is typically an integer but you should not assume that. This is equivalent to $DBI::err or $h->err.
errstr
$str = $h->errstr; or $str = $DBI::errstr or $str = $h->errstr
Returns the native database engine error message from the last DBI method called. This has the same lifespan issues as the "err" method described above. This is equivalent to $DBI::errstr or $h->errstr.
rows
$rv = $h->rows; or $rv = $DBI::rows
This returns the number of rows effected by previous SQL statement and equivalent to $DBI::rows.
trace
$h->trace($trace_settings);
DBI sports an extremely useful ability to generate runtime tracing information of what it's doing, which can be a huge time-saver when trying to track down strange problems in your DBI programs. You can use different values to set trace level. These values varies from 0 to 4. The value 0 means disable trace and 4 means generate complete trace.
Interpolated Statements are Prohibited
It is highly recommended not to use interpolated statements as follows −
while ($first_name = <>) {
my $sth = $dbh->prepare("SELECT *
FROM TEST_TABLE
WHERE FIRST_NAME = '$first_name'");
$sth->execute();
# and so on ...
}
Thus don't use interpolated statement instead use bind value to prepare dynamic SQL statement.