
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Path Testing & Basis Path Testing with Example
Basis Path Testing is a white-box testing technique based on a program's or module's control structure. A control flow graph is created using this structure, and the many possible paths in the graph are tested using this structure.
The approach of identifying pathways in the control flow graph that give a foundation set of execution paths through the program or module is known as basis path testing.
Because this testing is dependent on the program's control structure, it necessitates a thorough understanding of the program's structure. Four stages are followed to create test cases using this technique −
Create a Control Flow Graph.
Calculate the Graph's Cyclomatic Complexity
Identify the Paths That Aren't Connected
Create test cases based on independent paths.
Control Flow Graph
A control flow graph (or simply flow graph) is a directed graph that depicts a program's or module's control structure. V number of nodes/vertices and E number of edges make up a control flow graph (V, E). A control graph can also include the following −
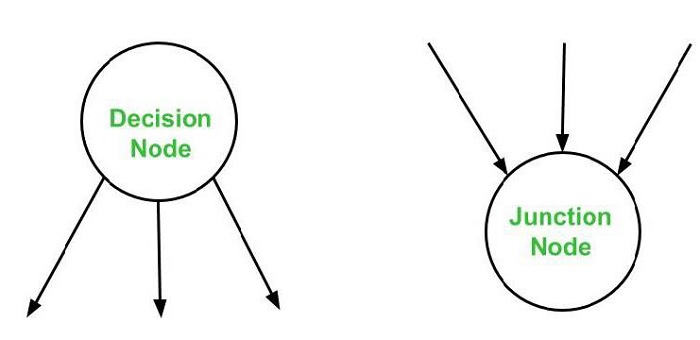
A node with multiple arrows entering it is known as a junction node.
A node having more than one arrow leaving it is called a decision node.
The area encompassed by edges and nodes is referred to as a region (area outside the graph is also counted as a region.).
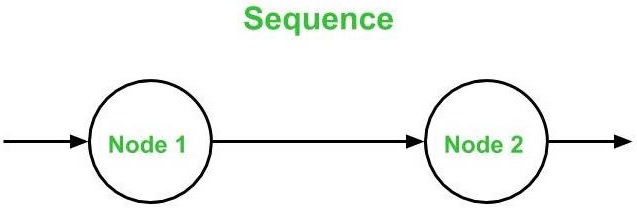
Below are the notations utilized while constructing a flow graph −
- Sequential Statements −
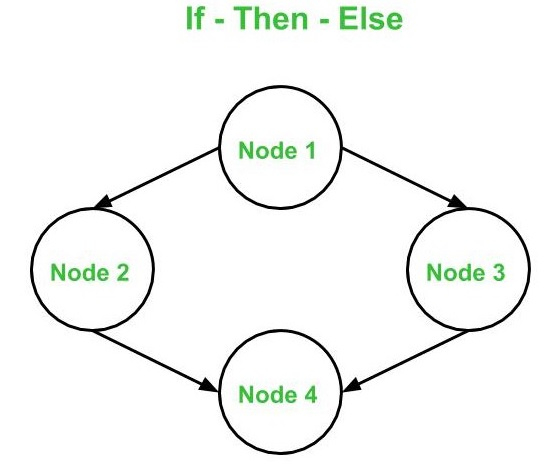
- If – Then – Else
- Do – While
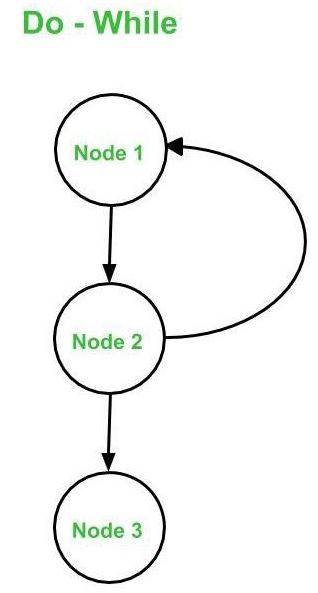
- While – Do
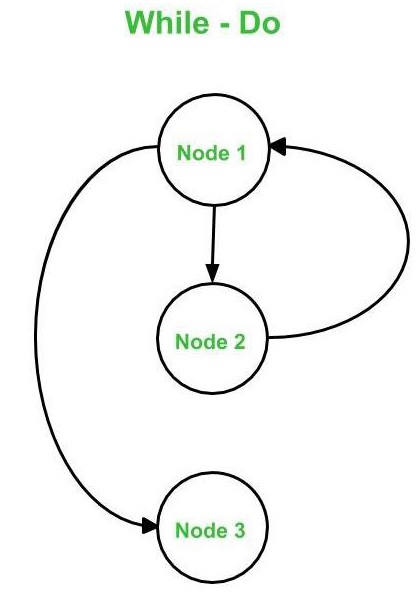
- Switch – Case
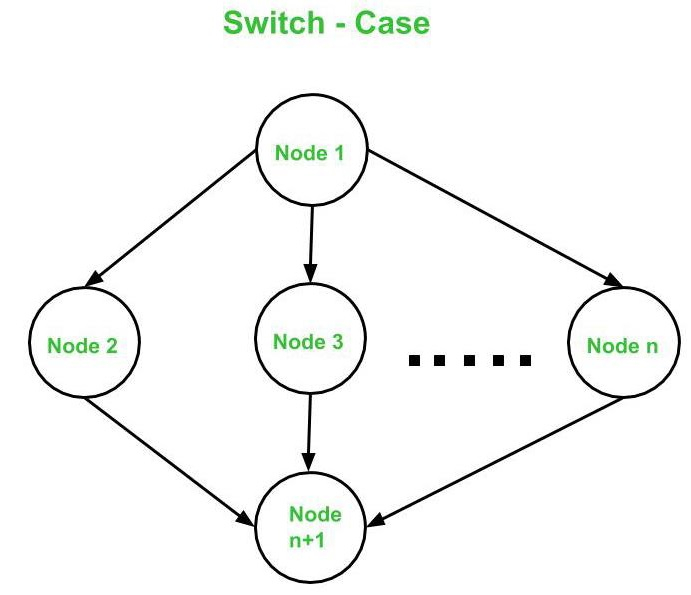
Cyclomatic Complexity
The cyclomatic complexity V(G) is said to be a metric for a program's logical complexity. Three distinct formulas can be used to compute it −
V(G) = e - n + 2*P is a formula based on edges and nodes.
Where e is the number of edges, n denotes the number of vertices, and P denotes the number of connected components.
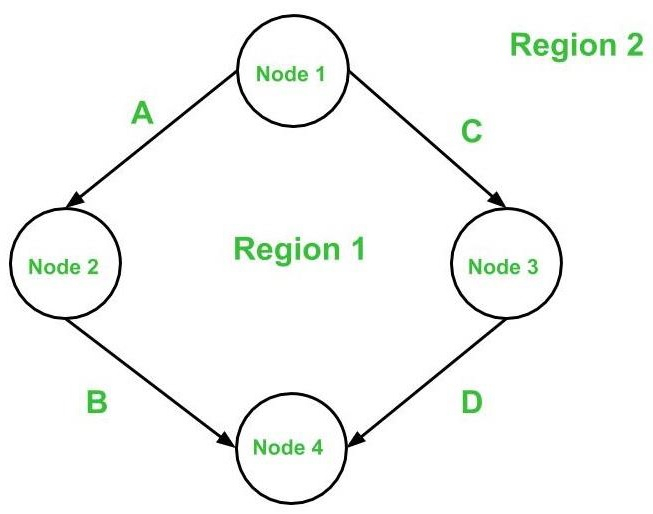
Take, for example, the first graph shown above.
where e = 4, n = 4, and p = 1 are all integers
V(G) = 4 - 4 + 2 * 1 = 2 cyclomatic complexity
The following is a formula based on Decision Nodes −
V(G) = d + P, where d represents the number of decision nodes and P represents the number of connected nodes.
Take, for example, the first graph shown above.
where d=1 and p=1
V(G) = 1 + 1 = 2 cyclomatic complexity
The following is a formula based on regions −
V(G) denotes the number of graph regions.
Take, for example, the first graph shown above.
V(G) = 1 (for region 1) + 1 (for region 2) = 2 cyclomatic complexity
As a result, the cyclomatic complexity derived using all three formulas remains the same. These three equations can be used to compute and validate the flow graph's cyclomatic complexity.
Observation
Only one flow graph is created for each function [e.g. Main( ) or Factorial() ]. If there are many functions in a program, a separate flow graph is created for each of them. In addition, the value of ‘p' in the cyclomatic complexity formula is determined by the total number of graphs.
If there are exactly two arrows leaving a decision node, it is counted as one decision node. If there are more than two arrows leaving a decision node, the following formula is used −
d = k - 1
The number of arrows leaving the decision node is given by k.
Independent Path
In the control flow graph, an independent path is one that introduces at least one new edge that has not been traversed before the path is created. The cyclomatic complexity of a flow graph is the number of independent pathways present. This is because the cyclomatic complexity is used as an upper limit for the number of tests that should be run to ensure that all of the program's statements have been run at least once.
In the first graph, the number of independent paths is equal to the cyclomatic complexity, hence the number of independent paths is 2.
So, in the above-mentioned first graph, the independent pathways are −
- A -> B is the first path.
- C is the second path.
Note − It's worth noting that independent paths aren't necessarily unique. In other words, if the cyclomatic complexity of a graph is N, there is a chance of finding two distinct sets of pathways, each of which is independent in nature.
Finally, once the separate paths have been obtained, test cases can be constructed, with each test case representing one or more independent paths.
Examples of Path Testing
In the previous post, we looked at the stages involved in creating test cases for a program utilizing base path testing. Let's now solve an example using the same steps.
Consider the following program, which determines whether an integer is prime or not. The following is the schedule for the following program −
Create a Control Flow Diagram.
Calculate the cyclic complexity using all of the methods available.
Create a list of all the Independent Paths Design test cases.
int main (){
int n, index;
cout << "Enter a number: " << endl;
cin >> n;
index = 2;
while (index <= n - 1) {
if (n % index == 0) {
cout << "It is not a prime number" << endl;
break;
}
index++;
}
if (index == n)
cout << "It is a prime number" << endl;
} // end main
Solution: 1. Create a Control Flow Diagram
Step 1 − After declaring the variables, begin numbering the statements (if no variables have been initialized in that statement). If a variable is initialized and declared on the same line, however, the numbering should begin on that line.
This is how numbering will be done for the supplied program −
int main (){
int n, index;
cout << "Enter a number: " <> n;
index = 2;
while (index <= n - 1){
if (n % index == 0){
cout << "It is not a prime number" << endl;
break;
}
index++;
}
if (index == n)
cout << "It is a prime number" << endl;
} // end main
Step 2 − Combine all of the sequential statements into one node. Statements 1, 2, and 3 are, for example, all consecutive statements that should be concatenated into a single node. For the rest of the statements, we'll use the notations described here.
Note − To keep things simple, number nodes in alphabetical order.
The resulting graph will look like this −
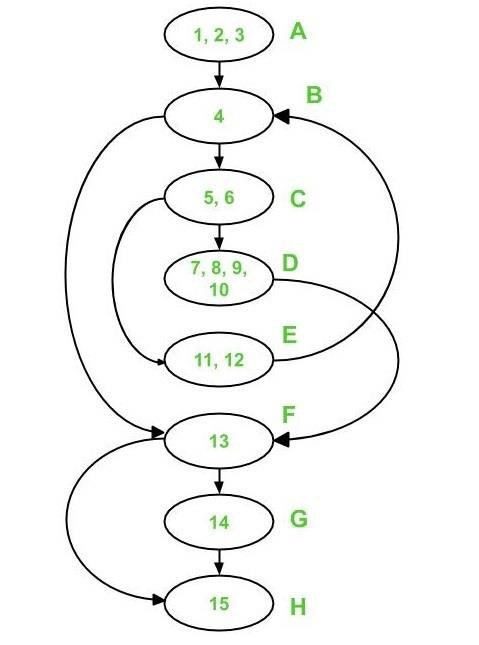
Calculate the cyclomatic complexity by using the following formula −
Method 1:
V(G) = e - n + 2*p
In the control flow diagram above,
where e = 10, n = 8, and p =1
As a result, V(G) = 10 - 8 + 2 * 1 = 4 Cyclomatic Complexity
Method 2:
V(G) = d + p
In the control flow diagram above,
where d = 3 (Node B, C, and F) and p = 1
As a result, the cyclomatic complexity V(G) = 3 + 1 = 4
Method 3:
V(G) = Number of Regions (method 3)
There are four zones in the aforementioned control flow graph, as indicated below −
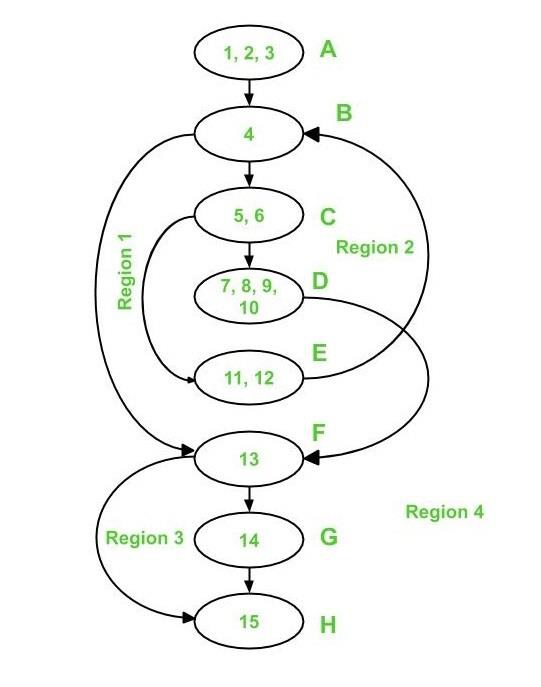
As a result, there are four distinct regions: R1, R2, R3, and R4.
V(G) = 1 + 1 + 1 + 1 = 4 cyclomatic complexity
It's worth noting that all three ways get the same cyclomatic complexity V value (G).
Independent Paths
Because the cyclomatic complexity V(G) for the graph is 4, there are 4 independent paths.
Path 1 covers (in red) the following edges −
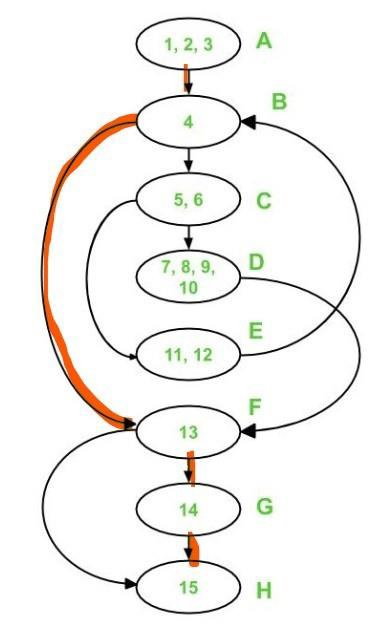
A – B – F – G – H is the first path.
The following are the edges that Path 1 and Path 2 cover −
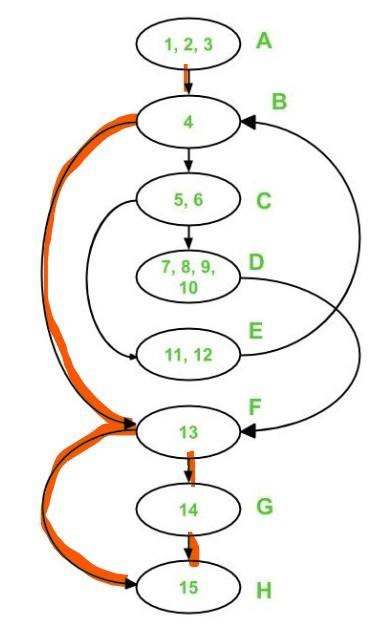
A – B – F – H is the second path.
Path 1, Path 2, and Path 3 cover the following edges −
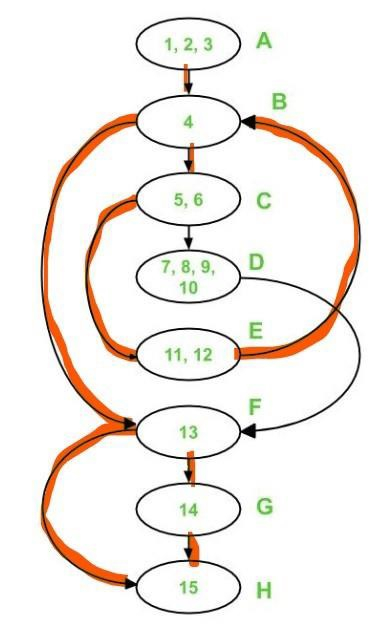
A - B - C - E - B - F - G - H is the third path
Only two edges remain uncovered, namely edge C-D and edge D-F. As a result, these two edges must be included in Path 4.
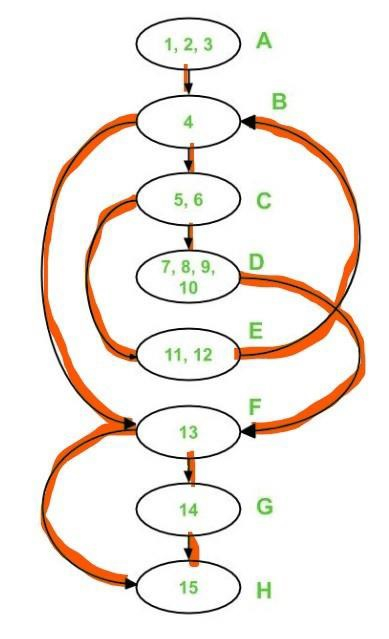
A - B - C - D - F - H is the fourth path.
Each of these pathways has at least one new edge that has never been crossed previously.
Note that independent pathways aren't always unique.
Test Cases
We must use the previously discovered independent paths to generate test cases. Provide input to the program in such a way that each independent path is executed to create a test case.
The following test cases will be obtained for the supplied program −
| Test case ID |
Input Number |
Output |
Independent Path covered |
|---|---|---|---|
| 1 |
1 |
No output |
A-B-F-H |
| 2 |
2 |
It is a prime number |
A-B-F-G-H |
| 3 |
3 |
It is a prime number |
A-B-C-E-B-F-G-H |
| 4 |
4 |
It is not a prime number |
A-B-C-D-F-H |
Advantages of Basis Path Testing
Basis Path Testing is useful in the following situations −
Additional Coverage − Because it focuses on maximum logic coverage rather than maximal path coverage, basis path testing gives the best code coverage. As a result, the code is well tested overall.
Testing for Maintenance − When a piece of software is modified, it's still required to test the changes made, which necessitates path testing.
When a developer produces code, the first thing he or she does is test the program's or module's structure. As a result, base path testing necessitates a thorough understanding of the code's structure.
Testing for Integration − There is a considerable risk of Interface problems when one module calls another. Path testing is used to test all of the pathways on the interfaces of the modules in order to avoid such problems.
Testing effort − Because the cyclomatic complexity of software (i.e., a program or module) is computed using the basis path testing technique, it is obvious to observe that the testing effort in basis path testing is directly related to the complexity of the software or program.

