Non-Negative Matrix Factorization

Introduction

Non-Negative Matrix Factorization (NMF) is a supervised algorithm used to represent data into lower dimensions which reduces the number of features while preserving enough basic information to construct the original matrix from the reduced feature space.

In this article, we will be going explore more about NMF and how it can be useful.

Non-Negative Matrix Factorization

NMF is used to reduce the dimensions of the input matrix or corpus. It uses factor analysis which gives less importance to less relevant words. The decomposition of the original matrix(which is a non-negative matrix) thus creates a product of two non-negative coefficients with a rank lower than that of the original matrix.

Importance of NMF

• NMF belongs to the category of algebra-based algorithms that are used to determine the hidden state.

• It can be used for topic modeling TF-IDF.

• NMF can easily extract sparsely populated data and factors.

Below is a representation of Non-Negative matrix factorization in topic modeling

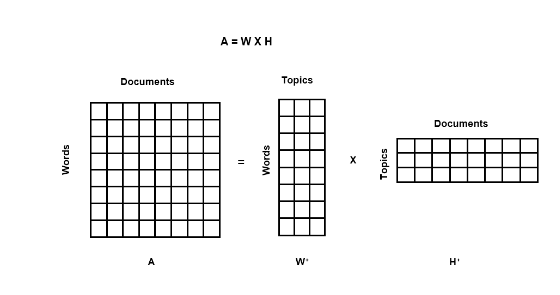
Matrix 1 (H+): Topic and words

Matrix 3 (W+): Documents and topics

Representation of NMF

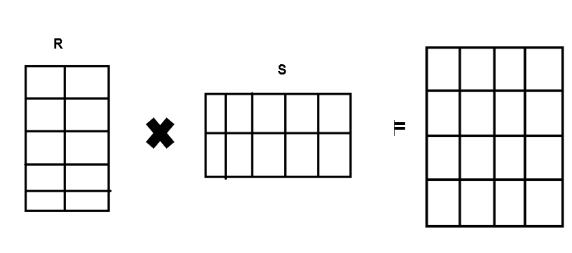
Let us have one input matrix M of shape p x q. The matrix factorization topic modeling will decompose the matrix M into two matrices R and S of shapes p x t and t x q.

Thus, we have three matrices as described below.

Matrix M − shape (p x q) Represents the document term matrix

Matrix R − shape (p x t ) Represents the word embedding matrix

Matrix S − shape (t x q ) Weight of each word in a sentence is represented in each column

Mathematic modeling of NMF

NMF is an unsupervised ML technique that computes the distance between the elements. There are different methods to calculate the distance. Two such methods are discussed below.

• KL Divergence − It is used to determine the closeness of two distributions on quantitative aspects. Thus, if two words are similar and close the value of KL divergence tends to zero otherwise it increases.

The general formula for KL Divergence is given as

$$\mathrm{D_{K\:L}(p(x)||q\left ( x \right ))=\sum _{x\epsilon X}p(x)ln\frac{p(x)}{q(x))}}$$

• Euclidean Distance - The distance between two points in space can be given as

$$\mathrm{d(p,q)=\sqrt{(q_{1}-p_{1})^{2}+(q_{2}-p_{2})^{2}}}$$

Advantages of Non-Negative Matrix Factorization

• It can handle missing data while minimizing the cost function and does not consider missing data as zeros.

• It can work by breaking down a higher-complex matrix into a lower-dimension matrix. It is considered better than LDA.

Conclusion

Non Negative matrix Factorization is a widely used technique for dimension reduction, especially in fields related to Natural Language and Machine Learning. It is faster, and easier and produces better results than those of its rivals like LDA.