Minimum steps in which N can be obtained using addition or subtraction at every step

From the above problem statement, our task is to get the minimum steps in which a given number N can be obtained using addition or subtraction at every step. We can understand that we need to print the minimum number of steps that we can perform and sequence of the steps on any given integer N to reach the number starting from 0 by addition or subtraction of the step number.

In this problem set, we can add or subtract the number equal to the step count from the current location at each step. For instance, we can add either 1 or -1 at step 1. Further moving forward we can add 2 or -2 at step 2 and so on. We can add or subtract to the number at every step depending on the situation.

The main challenge of the problem is that we need to perform the minimum steps to reach N, starting from 0. Let’s understand the problem better with an example.

The below given example will illustrate to you every number we can reach with 2 steps starting from 0 by carrying out the stated operations.

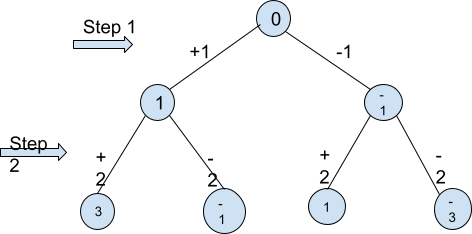
For example, let’s say if we are given N=1.

Output

Minimum no of steps: 1
Sequence of steps: 1

Explanation

We can reach 1 by two ways −

• By simply adding 1 to move from 0 to 1 at step 1, which requires 1 step.

• By subtracting 1 to move from 0 to -1 at step 1 and then adding 2 to move from -1 to 1 at step 2, which requires 2 steps.

Since the problem states we need minimum steps to reach any number N, so the desired output for this input will be 1.

For, N=3

Output

Minimum no of steps: 2
Sequence of steps: 1 2

Explanation

We add 1 to move from 0 to 1 at step 1 and then add 2 to move from 1 to 3 at step 2.

Approach

The best way to solve the problem is to first figure out if N is a positive or negative number. We must add or subtract at the appropriate step numbers respectively to solve the problem.

• If N is a positive number, keep adding the step numbers until the total sum exceeds or equals to N.

• Similarly if N is a negative number, keep subtracting the step numbers until the total sum exceeds or equals N.

• If in the above cases total sum equals N return the number of steps and sequence of steps. The main problem is to deal with the situation when it exceeds N.

Once the total sum surpasses N, check whether (sum-N) is even or odd.

• If (sum-N) is even, then we must perform subtraction at (sum-N)/2 step to reach N.

  Let’s understand this case better with a suitable example.

  For, N=8

  1+2+3+4=10, it exceeds 8.

  Since 10-8=2 which is an even number. So we will subtract at 2/2 step i.e

  Step 1. Hence, the sequence of the steps will be -1 2 3 4 and the minimum

  number of steps to reach N will be 4.

• If (sum-N) is an odd number, first we will determine whether the previous step at which total sum surpassed the number N was even or odd.

  If the previous step is an odd number, perform one more step by adding the next step number which will give us (sum-N) as an even number and then perform the above steps to get the desired result.

  For example, N=9

  1+2+3+4=10, which exceeds 9.

  Since 10-9=1, which is an odd number. The next step is 5 which is an odd number so we will just perform one step by adding 5 to the total sum which will give 15 making (sum-N)=6. Performing subtraction at step 3 will give the sequence 1 2 -3 4 5, which is the desired output.

  Let’s assume if the previous step is an even number, in this case we need to perform two steps by adding the i th step and subtracting (i+1)th step to give (sum-N) as an even number to get the required sequence of steps.

  For N=5

  1+2+3=6, which exceeds 5.

  Since (sum-N) =1 so we will consider the last step when su surpasses the number N. Since it is even we will perform two steps i..e 4th step and 5th step. Our task is to make (sum-N) even so by adding at 4th step and subtracting at 5th step we can make (sum-N) even as it will subtract 1 from the total sum. Since (sum-N) equals 0, we reach N. Hence, the sequence is 1 2 3 4 -5.

Example

Below is the C++ code for the approach −

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
   vector <int> steps; // for storing the sequence
   int totalSum=0; 
   int temp=0;
   if(n>=0){   // if n is positive then temp will store positive
      temp=1;
   } else {
      temp=-1;  // n is negative then temp will store negative
   }
   n=abs(n);
   int step=0;
   for(step=1;totalSum<n;step++){  // for storing the steps till sum is not greater than n
      steps.push_back(temp*step);
   
      totalSum=totalSum+step;
   }
   if(totalSum>temp*n) {  //when sum greater than n 
      if(step%2==0) {   //when step is even 
         totalSum=totalSum-n; 
         if((totalSum)%2!=0) { // when totalSum-n is odd
            steps.push_back(temp*step);  //store the addition of next step 
            steps.push_back((temp*-1)*(step+1));  // store the subtraction of next step 
            totalSum--;  //make totalSum even
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1; 
		} else {        //when step is odd
         totalSum=totalSum-n;
         if((totalSum)%2!=0)  {  // when totalSum-n is odd 
            steps.push_back(temp*step);   //store the next addition value 
            totalSum+=step; 
            step++;
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1;
   
      }
   }
   //print the minimum number of steps taken 
   cout<<"The minimum number of steps : "<<steps.size()<<endl;
   //print the steps is stored in vector
      cout<<"Sequence of steps : ";
   for(int i=0;i<steps.size();i++){
      cout<<steps[i]<<" ";
   }
   
}
int main(){
   int m=17;
   minimumStep(m);
   
   return 0;
}

Output

The minimum number of steps : 6
Sequence of steps : 1 -2 3 4 5 6

Time Complexity: O(sqrt(N))

Space Complexity: O(sqrt(N))

Conclusion

In this article, we have tried to explain the approach to find out the minimum steps to reach N by adding or subtracting at every step and printing the sequence. I hope this article helps you to learn the concept in a better way.