Minimization of Incompletely Specified Logic Functions

In Boolean or logic algebra, a logic function is a mathematical expression which specifies the relationship between inputs and outputs of a logic circuit. Boolean functions can be classified into two types namely, completely specified logic functions and incompletely specified logic functions.

A completely specified logic function is one whose output is determined or defined for every possible combination of inputs, while a Boolean function whose output value is unspecified for at least one combination of inputs is called incompletely specified logic function.

In an incompletely specified logic function, the combinations of input variables for which the output is not defined are called don’t care combinations.

In this article, we will discuss the minimization of incompletely specified logic functions with the help of examples.

Example 1

Minimize the Boolean expression to its minimal form,

$$F\left ( A,B,C,D \right )=\sum m\left ( 0, 3, 7, 8, 9, 10, 11, 15 \right )+d\left ( 2,4 \right )$$

Solution

We can observe that the given Boolean function has two don’t cares, i.e. 2 and 4, hence it is an incompletely specified logic function. We can minimize this function using K-Map (Karnaugh Map) minimization technique.

The K-map representation of the given incompletely specified logic function is shown in Figure-1 below.

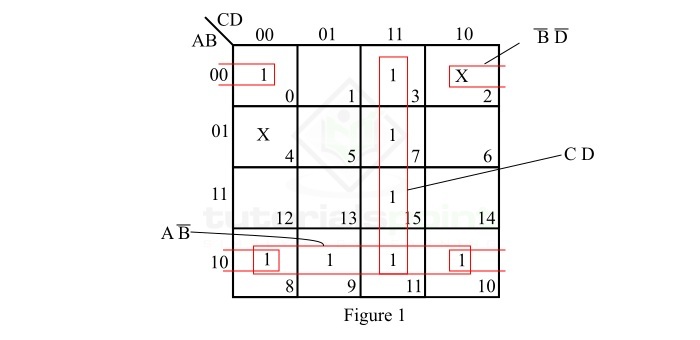
In the K-Map shown in Figure-1, the reduction is done as per the following steps −

• Step 1 − There are no isolated 1s.

• Step 2 − The minterm m₀ makes four square with minterms m₂ (don’t care), m₈, and m₁₀. Make the four square and read it as $\bar{B}\bar{D}$

• Step 3 − The minterm m₃ makes a four square with minterms m₇, m₁₁, and m₁₅. Make the four square and read it as $CD$.

• Step 4 − The minterm m₈ makes a four square with minterms m₉, m₁₀, and m₁₁. Make the four square and read it as $A\bar{B}$.

• Step 5 − Write all the product terms in SOP (Sum of Product) form.

Thus, the minimal SOP expression of the given incompletely specified logic function is,

$$F_{min}=\bar{B}\bar{D}+A\bar{B}+CD$$

Example 2

Minimize the following Boolean expression,

$$F\left ( A,B,C,D \right )=\sum m\left ( 1, 3, 7, 11, 15 \right )+d\left ( 0, 2, 5 \right )$$

Solution

We can observe that the given Boolean function has three don’t care minterms. Hence, it is an incompletely specified logic function.

Now, let us use the K-Map reduction technique to minimize this expression to the minimal form. The K-map representation of the given function is shown in Figure-2.

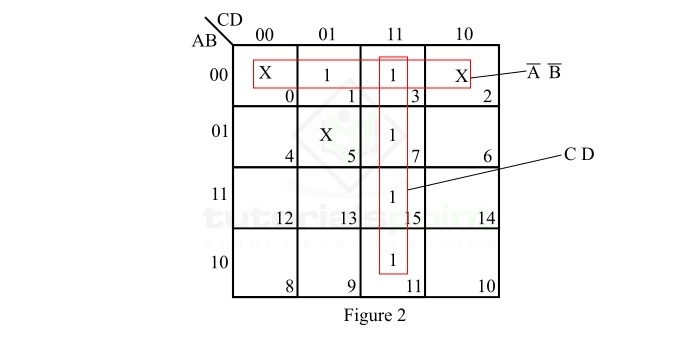
In the K-map shown in Figure-2, the minimization of the incompletely specified function is done as per the following steps −

• Step 1 − There are no isolated 1s.

• Step 2 − The minterm m1 forms a four square with minterms m₀ (don’t care), m₂ (don’t care), and m₃. Make this four square and read it as $\bar{A}\bar{B}$.

• Step 3 − The minterm m₇ makes a four square with minterms m₇, m₁₁, and m₁₅. Make this four square and read it as $CD$.

• Step 4 − Write all the product terms in SOP form.

So, the minimal Boolean expression of the given incompletely specified logic function is,

$$F_{min}=\bar{A}\bar{B}+CD$$

This is all about the minimization of incompletely specified logic functions in Boolean algebra.