
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Memorization (1D, 2D and 3D) Dynamic Programming in Java
Memorization is a technique based on dynamic programming which is used to improve the performance of a recursive algorithm by ensuring that the method does not run for the same set of inputs more than once by keeping a record of the results for the provided inputs(stored in an array).Memorization can be achieved by implementing top down approach of the recursive method.
Let us understand this scenario with the help of basic Fibonacci example
1-D Memorization
We will be considering a recursive algorithm with only one non constant parameter (only one parameter changes its value) hence this method is called 1-D memorization. The following code is to find N’th(all the terms till N) in the Fibonacci series.
Example
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}
Output
IF we run the above code with n=5, it will generate the following output.
Calculating fibonacci number for: 5 Calculating fibonacci number for: 4 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2 Calculating fibonacci number for: 2 Calculating fibonacci number for: 3 Calculating fibonacci number for: 2
Fibonacci value for n=5: 5
It is noticed that the Fibonacci number for 2 and 3 is calculated more than once.Let us better understand by drawing a recursive tree for the Fibonacci series of the above condition i.e n=5.
Here two children of node will represent the recursive call it makes. As can be seen F(3) and F(2) are calculated more than once and can be avoided with caching the results after each step.
We will be using an instance variable memoize Set for caching the result.It is first checked if n is already present in the memoize Set, if yes the value is returned, and if not the value is computed and added to the set.
Example
import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
public int fibMemoize(int input) {
if (input == 0)
return 0;
if (input == 1)
return 1;
if (this.memoizeSet.containsKey(input)) {
System.out.println("Getting value from computed result for " + input);
return this.memoizeSet.get(input);
}
int result = fibMemoize(input - 1) + fibMemoize(input - 2);
System.out.println("Putting result in cache for " + input);
this.memoizeSet.put(input, result);
return result;
}
public int fibonacci(int n) {
if (n == 0)
return 0;
if (n == 1)
return 1;
System.out.println("Calculating fibonacci number for: " + n);
return (fibonacci(n - 1) + fibonacci(n - 2));
}
public static void main(String[] args) {
TutorialPoint tutorialPoint = new TutorialPoint();
System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
}
}
Output
If we run the above code it will generate the following Output
Adding result in memoizeSet for 2 Adding result in memoizeSet for 3 Getting value from computed result for 2 Adding result in memoizeSet for 4 Getting value from computed result for 3 Adding result in memoizeSet for 5
Fibonacci value for n=5: 5
As can be seen the Fibonacci number for 2 and 3 are not calculated again. Here we introduce a HashMap memorizes to store the values which are already computed before every Fibonacci calculation is checked in the set if for the input the value has been calculated and if not the value for the particular input is added to the set.
2-D Memorization
The above program we had only one non constant parameter. In the below program we will take an example of a recursive program having two parameters which changes its value after every recursive call, and we will implement memorization on the two non-constant parameters to optimize it. This is called 2-D Memorization.
For Example:-We are going to implement standard Longest Common Subsequence(LCS).If a set of sequences are given, the longest common subsequence problem is to find a common subsequence of all the sequences that is of maximal length. The possible combinations will be 2n.
Example
class TP {
static int computeMax(int a, int b) {
return (a > b) ? a : b;
}
static int longestComSs(String X, String Y, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (X.charAt(m - 1) == Y.charAt(n - 1))
return 1 + longestComSs(X, Y, m - 1, n - 1);
else
return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
}
public static void main(String[] args) {
String word_1 = "AGGTAB";
String word_2 = "GXTXAYB";
System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
}
}
Output
If we run the above code it will generate the following Output
Length of LCS is 4
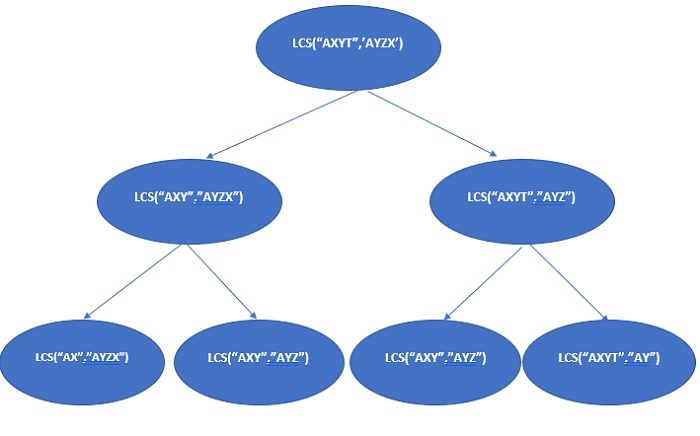
In the above halfway recursion tree, lcs("AXY", "AYZ") is solved more than once.
As a result of the Overlapping Substructure property of this problem, pre computation of the same sub problems can be avoided by using Memorization or Tabulation.
The Memorization approach of recursive code is implemented as follows.
Example
import java.io.*;
import java.lang.*;
class testClass {
final static int maxSize = 1000;
public static int arr[][] = new int[maxSize][maxSize];
public static int calculatelcs(String str_1, String str_2, int m, int n) {
if (m == 0 || n == 0)
return 0;
if (arr[m - 1][n - 1] != -1)
return arr[m - 1][n - 1];
if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
return arr[m - 1][n - 1];
}
else {
int a = calculatelcs(str_1, str_2, m, n - 1);
int b = calculatelcs(str_1, str_2, m - 1, n);
int max = (a > b) ? a : b;
arr[m - 1][n - 1] = max;
return arr[m - 1][n - 1];
}
}
public static void main(String[] args) {
for (int i = 0; i < 1000; i++) {
for (int j = 0; j < 1000; j++) {
arr[i][j] = -1;
}
}
String str_1 = "AGGTAB";
String str_2 = "GXTXAYB";
System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
}
}
Output
If we run the above code it will generate the following Output
Length of LCS is 4
Approach
It has been seen that in the method(calculatelcs) there are 4 arguments with 2 constant (which does not affect the Memorization) and 2 non-constant arguments (m and n) which changes its value in every recursive method calling. So to achieve Memorization we introduce a 2-D array to store the computed values of lcs(m,n) at arr[m-1][n-1]. We do not perform any more recursive calls and return arr[m-1][n-1] whenever the function with the same arguments m and n is called again, as the previous computation of the lcs(m, n) has already been stored in arr[m-1][n-1], thus minimizing the number of recursive calls.
3-D Memorization
This is a approach to achieve Memorization for a recursive program having 3 non-constant arguments. Here we are taking the example of computing the Length of LCS for three strings.
The approach here is to generate all possible subsequences (Total possible subsequences are 3?) for the given strings and match for the longest common subsequence among them.
We would be introducing a 3-D table to store the computed values. Considering the subsequences.
A1[1...i] i < N
A2[1...j] j < M
A3[1...k] k < K
If we find a common character(X[i]==Y[j]==Z[k]) we need to recur the remaining ones.Or else we will compute the maximum of the following cases
Leave X[i] recur for others
Leave Y[j] recur for others
Leave Z[k] recur for others
So, if we formulate the above idea in to our recursion function then
f(N,M,K)={1+f(N-1,M-1,K-1)if (X[N]==Y[M]==Z[K]maximum(f(N-1,M,K),f(N,M-1,K),f(N,M,K-1))}
f(N-1,M,K) = Leave X[i] recur for others
f(N,M-1,K) = Leave Y[j] recur for others
f(N,M,K-1) = Leave Z[k] recur for others
Example
import java.io.IOException;
import java.io.InputStream;
import java.util.*;
class testClass {
public static int[][][] arr = new int[100][100][100];
static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
arr[i][j][0] = 0;
}
}
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= o; j++) {
arr[0][i][j] = 0;
}
}
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= o; j++) {
arr[i][0][j] = 0;
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 1; k <= o; k++) {
if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
}
else {
arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
}
}
}
}
return arr[m][n][o];
}
static int calculateMax(int a, int b, int c) {
if (a > b && a > c)
return a;
if (b > c)
return b;
return c;
}
public static void main(String[] args) {
String str_1 = "clued";
String str_2 = "clueless";
String str_3 = "xcxclueing";
int m = str_1.length();
int n = str_2.length();
int o = str_3.length();
System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
}
}
Output
If we run the above code it will generate the following Output
Length of LCS is 4

