Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum mirrors which can transfer light from bottom to right in C++
We are given with a square matrix which contains 0’s and 1’s only. 0 represents a blank or empty place and 1 means obstacle. We must find a number of mirrors that can be placed at empty cells such that these mirrors can transfer light from bottom to right. This is possible when, mirror is placed at index [i,j] and for all cells on the right in that particular row ( i ) and cells in the bottom ( j ) in that particular column have no obstacle.
If the mirror is at A[i][j], then all A[i+1 to n][ j ] and A[ i ][ j+1 to n ] are empty i.e, 0. As shown in below figure.
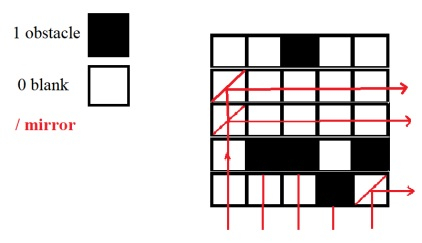
Input
Arr[][] = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,1,1,0,1},{1,1,1,0,1}}Output
No. of mirrors : 3
Explanation − As shown in figure. Mirrors can be placed at cells
Arr[1][0] − row 1 and column 0 has all 0’s below and right of it.
Arr[2][0] − row 2 and column 0 has all 0’s below and right of it.
Arr[4][4] − Last cell, is 0 and no rows below and column on right.
Approach used in the below program is as follows
Array Arr[][] is used to represent matrix of 0’s and 1’s..
Function maximumMirror(int mat[][], int n) takes matrix and it’s side n as input and returns the count of maximum mirrors that can be placed as shown above.
Variable flag is used to mark the presence of an obstacle in cells below or cells on the right of arr [i] [j].
Count is used to represent the number of mirrors, initially 0 .
Traverse matrix from index 0,0.
For each cell if it is empty (mirror can be placed), check for cells below( k=i+1 to n-1) . If any arr[k][j] is an obstacle (value=1 ) then break while loop and mark flag as 1. If not, continue checking for cells in right ( l=j+1 to n-1 ).
Set flag in case an obstacle is present.
After both while loops if flag is 0 then increment count as mirror can be placed.
Return count as no. of mirrors that is maximum.
Example
// C++ program to find how many mirrors can transfer
// light from bottom to right
#include <bits/stdc++.h>
using namespace std;
// method returns number of mirror which can transfer
// light from bottom to right
int maximumMirror(int mat[5][5], int N){
// to mark that all cells in the right or bottom are 0---no obstacle
int flag=0;
int count=0; //count of mirrors
int i,j,k,l;
//for all cells
for (int i=0; i<N; i++)
for(j=0;j<N;j++){
//check from next column and next row
int k=i+1;
int l=j+1;
if(mat[i][j]==0) //position for mirror{
while(k<N) //check for rows below{
if(mat[k][j]==1) //keeping column fixed, if there is obstacle break{
flag=0; break; }
else
flag=1;
k++;
}
if(flag==1) //if no obstacle in rows then check columns in right
while(l<N) //checking for columns in right{
if(mat[i][l]==1) //keep row fixed, if obstacle break{
flag=0; break;
}
else
flag=1;
l++;
}
if(flag==1) //there is no obstacle for mirror mat[i][j]
count++;
}
}
return count;
}
int main(){
int N = 5;
//matrix where 1 represents obstacle form 5X5 matrix
int mat[5][5] = {{0,0,1,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,1,1,0,1},{1,1,1,0,1}};
cout <<"Maximum mirrors which can transfer light from bottom to right :"<<
maximumMirror(mat, N) << endl;
return 0;
}Output
Maximum mirrors which can transfer light from bottom to right :3
48 Views
