Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum and minimum isolated vertices in a graph in C++
We are given with the number of edges Noe and number of vertices Nov. The goal is to find the minimum and maximum number of isolated vertices that are possible in such graphs which have no edges and No vertices count.
An isolated vertex is the one that has no edge connected to it.
- For minimum isolated vertices
We will make sure that every edge is isolated. ( No two edges have common vertices ) Each edge requires only 2 vertices. So ,
count of non isolated vertices = 2 * no. of edges
count of isolated vertices = total vertices - count of non isolated vertices.
If the no. of vertices is <= 2 * no. of edges, means all vertices have a edge connected. So no. of isolated vertices is 0.
- For maximum isolated vertices
For this we will try to make a polygon such that all edges are connected with minimum vertices.This is possible when we have a polygon such that each vertex pair also has diagonal between them.
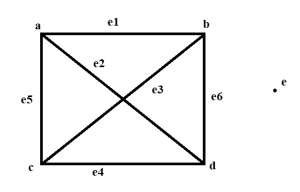
For given 5 vertices and 6 edges, the square is the polygon that has 6 edges with 2 diagonals so that only 4 vertices are occupied. 1 vertex becomes isolated and it is maximum.
No. of diagonals from one vertex to other in n sided polygon is n*(n-3)/2. Total edges=n*(n-1)/2
Input
No. of vertices 5, edges 6
Output
Minimum isolated vertices 0. Maximum isolated vertices 1.
Explanation
As shown in above figure.
Input − no. of vertices 2, edges=1
Output − Minimum isolated vertices 0. Maximum isolated vertices 0.
Explanation − An edge is formed between at least two vertices.
Approach used in the below program is as follows
The integers noe and nov contains the no. of edges and vertices.
Function findisolatedvertices(int v, int e) takes of edges and vertices as parameters and prints the minimum and maximum isolated vertices possible.
If no. of vertices is <= 2*e, means no isolated vertex. Else non isolated vertices are 2*e (maximum), so minimum isolated will be v-2*e.
For calculating maximum isolated vertices, start from i=1 to no. of vertices, if (i * (i - 1) / 2 >= e) break as only i vertices are sufficient for e edges.
i stores the maximum isolated vertices possible.
Example
#include <bits/stdc++.h>
using namespace std;
void findisolatedvertices(int v, int e){
//one edge has 2 vertices
if (v <= 2 * e) //means all veritces have a connected edge
cout << "Minimum no. of isolated vertices: " << 0 << endl;
else {
int niso=2*e; //maximum non isolated vertices
cout << "Minimum no. of isolated vertices: " << v - niso << endl;
}
// To find out maximum number of isolated
// vertices
// Loop to find out value of number of
// vertices that are connected
int i;
for (i = 1; i <= v; i++) {
if (i * (i - 1) / 2 >= e)
break;
}
cout <<endl<< "Maximum no. of isolated vertices: " <<v-i;
}
int main(){
// Number of vertices
int nov = 5;
// Number of edges
int noe = 2;
// Calling the function to maximum and
// minimum number of isolated vertices
findisolatedvertices(nov, noe);
return 0;
}Output
Minimum no. of isolated vertices: 1 Maximum no. of isolated vertices: 2
319 Views
