Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Little Oh Notation (o)
Little o Notations
There are some other notations present except the Big-Oh, Big-Omega and Big-Theta notations. The little o notation is one of them.
Little o notation is used to describe an upper bound that cannot be tight. In other words, loose upper bound of f(n).
Let f(n) and g(n) are the functions that map positive real numbers. We can say that the function f(n) is o(g(n)) if for any real positive constant c, there exists an integer constant n0 ≤ 1 such that f(n) > 0.
Mathematical Relation of Little o notation
Using mathematical relation, we can say that f(n) = o(g(n)) means,
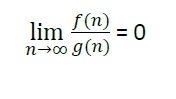
Example on little o asymptotic notation
If f(n) = n2 and g(n) = n3 then check whether f(n) = o(g(n)) or not.
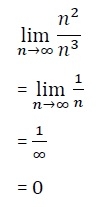
The result is 0, and it satisfies the equation mentioned above. So we can say that f(n) = o(g(n)).
Updated on: 05-Aug-2019
18K+ Views
Advertisements