Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Line/Edge Covering
A covering graph is a subgraph which contains either all the vertices or all the edges corresponding to some other graph. A subgraph which contains all the vertices is called a line/edge covering. A subgraph which contains all the edges is called a vertex covering.
Line Covering
Let G = (V, E) be a graph. A subset C(E) is called a line covering of G if every vertex of G is incident with at least one edge in C, i.e.,
deg(V) ≥ 1 ∀ V ∈ G
because each vertex is connected with another vertex by an edge. Hence it has a minimum degree of 1.
Example
Take a look at the following graph −
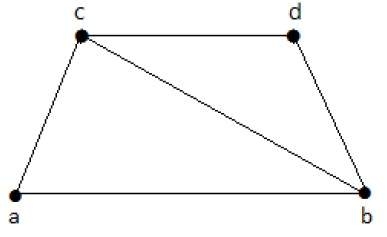
Its subgraphs having line covering are as follows −
C1 = {{a, b}, {c, d}}
C2 = {{a, d}, {b, c}}
C3 = {{a, b}, {b, c}, {b, d}}
C4 = {{a, b}, {b, c}, {c, d}}Line covering of 'G' does not exist if and only if 'G' has an isolated vertex. Line covering of a graph with 'n' vertices has at least [n/2] edges.
Minimal Line Covering
A line covering C of a graph G is said to be minimal if no edge can be deleted from C.
Example
In the above graph, the subgraphs having line covering are as follows −
C1 = {{a, b}, {c, d}}
C2 = {{a, d}, {b, c}}
C3 = {{a, b}, {b, c}, {b, d}}
C4 = {{a, b}, {b, c}, {c, d}}Here, C1, C2, C3 are minimal line coverings, while C4 is not because we can delete {b, c}.
Minimum Line Covering
It is also known as Smallest Minimal Line Covering. A minimal line covering with minimum number of edges is called a minimum line covering of 'G'. The number of edges in a minimum line covering in 'G' is called the line covering number of 'G' (α1).
Example
In the above example, C1 and C2 are the minimum line covering of G and α1 = 2.
Every line covering contains a minimal line covering.
Every line covering does not contain a minimum line covering (C3 does not contain any minimum line covering.
No minimal line covering contains a cycle.
If a line covering 'C' contains no paths of length 3 or more, then 'C' is a minimal line covering because all the components of 'C' are star graph and from a star graph, no edge can be deleted.
201 Views
