Length of Longest Common Subsequence Containing Vowels

In this problem, our task is to find the length of the longest possible subsequence present in two strings such that every letter of the subsequence must be a vowel. With the help of the recursive algorithm and iterative algorithm, the given problem statement can be solved. In English Alphabet, there exist five vowels named 'A', 'E', 'I', 'O', 'U'. Subsequence Vs. Substring: In Subsequence, we may take characters in a non-continuous way, but in Substring, we can take only continuous characters.

Ex: In String “TutorialsPoint”: “tri” is a subsequence but not a substring. While “tor” is both subsequence and substring.

To show you some instances

Instance-1

String 1: “point”

String 2: “tutorials”

Length of Common Subsequence containing vowels: 2

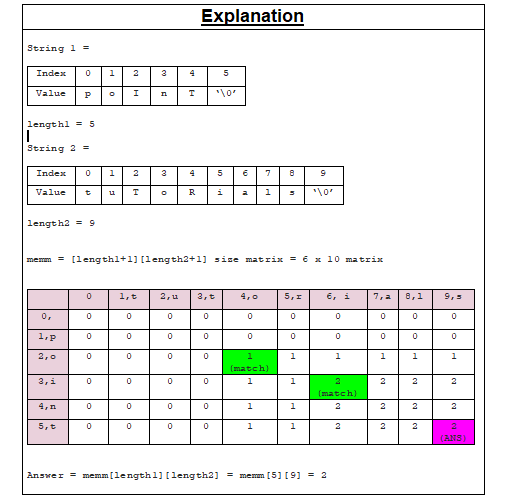
Instance-2

String 1: “longestsub”

String 2: “ohbekhfuo”

Length of Common Subsequence containing vowels: 3

Recursive Substructure

If idx_1 = 0 or idx_2 = 0, Then
	LCSVowels(idx1, idx2) = 0
Else If str1[idx_1-1] = str2[idx_2-1] and str1[idx_1-1] = Vowel, Then
	LCSVowels(idx_1, idx_2) = 1 + LCSVowels(idx_1-1, idx_2-1)
Else
	LCSVowels(idx_1, idx_2) = max(LCSVowels(idx_1, idx_2-1), LCSVowels(idx_1-1, idx_2))

Multiple Approaches

We have provided the solution in different approaches.

• Iterative Algorithm.

• Recursive Algorithm.

Approach-1: Iterative Algorithm

This is a Dynamic Programming approach based on Iterative Algorithm.

Algorithm: LCSVowels(string1, string2)

Step-1: length1 = LENGTH(string1)

Step-2: length2 = LENGTH(string2)

Step-3: Create 2-D integer Array “memm” of size (length1+1) X (length2+1).

Step-4: SET all columns of the first row = 0.

Step-5: SET all rows of the first column = 0.

Step-6: Use for loop LOOP (idx_1 = 1 to length1)

Step-7: Use inner LOOP(idx_2 = 1 to length2)

Step-8: Check the condition IF (string1[idx_1-1] == string2[idx_2-1] AND string1[idx_1-1] == VOWEL), THEN

Step-9: memm[idx_1][idx_2] = 1 + memm[idx_1-1][idx_2-1];

Step-10: otherwise memm[idx_1][idx_2]=MAX(memm[idx_1][idx_2-1],memm[idx_1-1][idx_2])

Step-11: RETURN memm[length1][length2]

Example

#include <iostream>
using namespace std;

/**
* @param ch: character parameter
*
* @return true: if ch == vowel
* @return false: if ch == consonent
*/
bool checkVowel(char chr) {
   switch(chr) {
       case 'A':
       case 'E':
       case 'I':
       case 'O':
       case 'U':
       case 'a':
       case 'e':
       case 'i':
       case 'o':
       case 'u':
           return true;
           break;
       default:
           return false;
           break;
   }
}

/**
* @param num1: first number
* @param num2: second number
*
* @return maximum number
*/
int maxx(int first, int second) {
   if (first >= second)
       return first;
   else
       return second;
}

/**
* @param string1: First String
* @param string2: Second String
*
* @return Length of maximum common subsequence containing vowels
*/
int LCSVowels(string string1, string string2) {
   int length1 = string1.length();
   int length2 = string2.length();
   // create memory array for using Dynamic Programming
   int memm[length1+1][length2+2];
   // make first column zero
   for (int idx_ = 0; idx_ <= length1; ++idx_) {
       memm[idx_][0] = 0;
   }
   // make first row zero
   for (int idx_=0; idx_ <= length2; ++idx_) {
       memm[0][idx_] = 0;
   }

   // traverse the DP matrix
   for (int idx_1=1; idx_1<=length1; ++idx_1) {
       for (int idx_2=1; idx_2<=length2; ++idx_2) {
           // if characters are equal and also they are vowels
           if (string1[idx_1-1] == string2[idx_2-1] && checkVowel(string1[idx_1-1])) {
               memm[idx_1][idx_2] = 1 + memm[idx_1-1][idx_2-1];
           } else {
               memm[idx_1][idx_2] = maxx(memm[idx_1][idx_2-1], memm[idx_1-1][idx_2]);
           }
       }
   }

   return memm[length1][length2];
}
int main() {
   string string1, string2;
     // Ask string 1
   cout << "Enter String 1: ";
   cin >> string1;
   // Ask String 2
   cout << "Enter String 2: ";
   cin >> string2;
   // call the function
   int lcs = LCSVowels(string1, string2);
   // display the result
   cout << "Length of Longest Common Subsequence containing vowels: " << lcs << endl;

   return 0;
}

Output

Enter String 1: point
Enter String 2: tutorials
Length of Longest Common Subsequence containing vowels: 2

Time Complexity of Program = O(length1 x length2)

Space Complexity of Program = O(length1 x length2)

Approach-2: Recursive Algorithm

This is a Dynamic Programming approach based on Recursive Algorithm.

Algorithm: LCS_Vowels(string1, string2, idx1, idx2, memm)

Step-1: IF (idx1 == -1 OR idx2 == -1), THEN RETURN 0

Step-2: IF (memm[idx1][idx2] != -1), THEN RETURN memm[idx1][idx2]

Step-3: IF (string1[idx_1] == string2[idx_2] AND string1[idx_1] == VOWEL), THEN

Step-4:memm[idx1][idx2] = 1 + LCS_Vowels(string1, string2, idx1-1, idx2-1, memm)

Step-5: Otherwise, set memm[idx1][idx2]=MAX(LCS_Vowels(string1, string2, idx1-1, idx2, memm)

, LCS_Vowels(string1, string2, idx1, idx2-1, memm))

Step-7: END IF

Step-8: RETURN memm[idx1][idx2]

Example

#include <iostream>
using namespace std;

/**
* @param ch: character parameter
*
* @return true: if ch == vowel
* @return false: if ch == consonent
*/
bool check_Vowel(char _chr) {
   switch(_chr) {
       case 'A':
       case 'E':
       case 'I':
       case 'O':
       case 'U':
       case 'a':
       case 'e':
       case 'i':
       case 'o':
       case 'u':
           return true;
           break;
       default:
           return false;
           break;
   }
}

/**
* @param num1: first number
* @param num2: second number
*
* @return maximum number
*/
int maxx(int first, int second) {
   if (first >= second)
       return first;
   else
       return second;
}

/**
* @param ABC: First String
* @param XYZ: Second String
* @param ABC_IDX: index for string-A
* @param XYZ_IDX: index for string-B
* @param memm: DP matrix
*/
int LCS_Vowels(string ABC, string XYZ, int ABC_IDX, int XYZ_IDX, int memm[1000][1000]) {
   if (ABC_IDX == -1 || XYZ_IDX == -1)
       return 0;

   if (memm[ABC_IDX][XYZ_IDX] != -1)
       return memm[ABC_IDX][XYZ_IDX];
  
   if (ABC[ABC_IDX] == XYZ[XYZ_IDX] && check_Vowel(ABC[ABC_IDX])) {
       memm[ABC_IDX][XYZ_IDX] = LCS_Vowels(ABC, XYZ, ABC_IDX-1, XYZ_IDX-1, memm) + 1;
   } else {
       memm[ABC_IDX][XYZ_IDX] = maxx(
           LCS_Vowels(ABC, XYZ, ABC_IDX-1, XYZ_IDX, memm),
           LCS_Vowels(ABC, XYZ, ABC_IDX, XYZ_IDX-1, memm)
       );
   }

   return memm[ABC_IDX][XYZ_IDX];
}

int main() {
   string ABC, XYZ;
  
   // Ask string 1
   cout << "Enter String 1: ";
   cin >> ABC;

   // Ask String 2
   cout << "Enter String 2: ";
   cin >> XYZ;

   int LENGTH_1 = ABC.length();
   int LENGTH_2 = XYZ.length();

   int memm[1000][1000];
   for (int p=0; p<1000; ++p) {
       for (int q=0; q<1000; ++q) {
           memm[p][q] = -1;
       }
   }

   // call the function
   int lcs = LCS_Vowels(ABC, XYZ, LENGTH_1-1, LENGTH_2-1, memm);

   // display the result
   cout << "Length of Longest Common Subsequence containing vowels: " << lcs << endl;

   return 0;
}

Output

Enter String 1: longestsub
Enter String 2: ohbekhfuo
Length of Longest Common Subsequence containing vowels: 3

Time Complexity of Program = O(length1 x length2)

Space Complexity of Program = O(length1 x length2)

Finally, this article depicts a c++ code for solving the given problem with the help of Dynamic Programming successfully. The algorithms use an O(length1 x length2) time complexity as well as space complexity for solving the problem.