Leibniz Harmonic Triangle

The Leibniz harmonic triangle, also known as Leibniz's series or the Leibniz formula, is a triangular arrangement of numbers discovered by German mathematician and philosopher Gottfried Wilhelm Leibniz in the late 17th century.

The Leibniz harmonic triangle is a triangular arrangement of fractions. We start at the top with the number and the outermost terms are reciprocal of the natural numbers depicting that particular row number. In general, a term in the leibniz harmonic triangle can be determined by the following equation, where r is the row number and c is the column number with the condition that c <= r

L(r,c)=L(r-1,c-1) - L(r,c-1), where L(r,1)=1/r

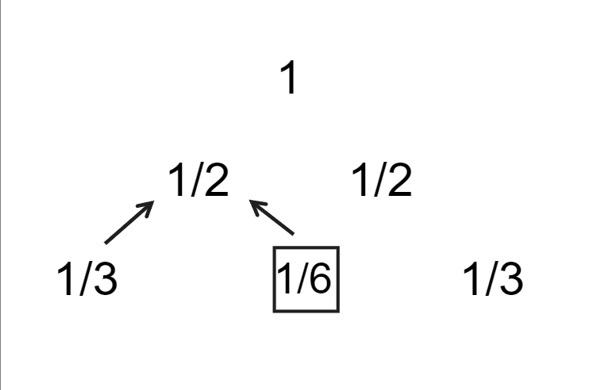
The following diagram depicts the first 3 rows of the Leibniz Harmonic Triangle.

Problem Statement

Given a number n, generate the Leibniz Harmonic Triangle for n rows.

Example

Input

n = 3

Output

1/1 
1/2 1/2 
1/3 1/6 1/3

Explanation

For n = 3, the Leibniz Harmonic Triangle has three rows. The outermost terms of each row = 1/(row number).

To generate this triangle, we start with the first row, which is 1/1. Then, for the second row, we calculate the value of each cell as the cell diagonally above and to the left minus the cell to the left:

L(2, 1) = 1/2

L(2, 2) = 1/2

So the second row is 1/2 1/2.

Finally, for the third row, we again calculate the value of each cell as the cell diagonally above and to the left minus the cell to the left

L(3,1) = L(3,3) = 1/3

L(3,2) = L(2,1) - L(3,1) = 1/6

Input

n = 4

Output

1/1 
1/2 1/2 
1/3 1/6 1/3 
1/4 1/12 1/12 1/4

Explanation

Uptill n = 3 the approach is the same as the above example.

For the fourth row

L(4,1) = L(4,4) = 1/4

L(4,2) = L(3,1) - L(4,1) = 1/3 - 1/4 = 1/12

L(4,3) = L(3,2) - L(4,2) = 1/6 - 1/12 = 1/12

Solution Approach

Pseudocode

• Start

• Initialize the value of n to 4.

• Declare a 2D vector L with n+1 rows and n+1 columns, and initialize all elements to 0.

• Call the function LHT with arguments n and L.

• Within the function LHT, iterate from i=0 to i<=n.

• Within the above loop, iterate from j=0 to j<=min(i,n).

• Within the above loop, if j==0 or j==i, set the value of L[i][j] to 1.

• Otherwise, set the value of L[i][j] to L[i-1][j-1]+L[i-1][j].

• Call the function printLHT with arguments n and L.

• Within the function printLHT, iterate from i=1 to i<=n.

• Within the above loop, iterate from j=1 to j<=i.

• Within the above loop, print "1/" followed by i*L[i-1][j-1].

• Print a new line after each inner loop completes.

• End.

Algorithm

function LHT()
    for i = 0 to n do
        for j = 0 to min(i, n) do
            if j == 0 or j == i then
                L[i][j] = 1
            else
                L[i][j] = L[i-1][j-1] + L[i-1][j]
            end if
        end for
    end for
    printLHT(n, L)
end function
function printLHT()
    for i = 1 to n do
        for j = 1 to i do
            print "1/" + i*L[i-1][j-1] + " "
        end for
        print new line
    end for
end function

function main
    Initialize n = 4
    L = 2D vector of size n + 1 x n + 1, with all elements initialized to 0
    LHT(n, L)
    return 0

Example: C++ Program

The following C++ Program generates and prints a Leibniz Harmonic Triangle for a given number of rows using the function LHT() and printLHT(). The main() function initializes the number of rows and creates a 2 dimensional vector ‘L’ of size n + 1 * n + 1 to store the terms.

// CPP Program to print Leibniz Harmonic Triangle
#include <bits/stdc++.h>
using namespace std;
// Function to print Leibniz Harmonic Triangle
void printLHT(int n, vector<vector<int>> L){
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= i; j++)
            cout << "1/" << i * L[i - 1][j - 1] << " ";
        cout << endl;
    }
}
// Function to generate Leibniz Harmonic Triangle
void LHT(int n, vector<vector<int>> &L){
    for (int i = 0; i <= n; i++){
        for (int j = 0; j <= min(i, n); j++){
            if (j == 0 || j == i)
                L[i][j] = 1;
            // Generate the value using previously stored values
            else
                L[i][j] = L[i - 1][j - 1] + L[i - 1][j];
        }
    }
    // print Leibniz Harmonic Triangle
    printLHT(n,L);
}
// Main function
int main(){
    int n = 5;
    // 2D vector to store the Leibniz Harmonic Triangle
    vector<vector<int>> L(n + 1, vector<int>(n + 1, 0));
    LHT(n, L);
    return 0;
}

Output

1/1 
1/2 1/2 
1/3 1/6 1/3 
1/4 1/12 1/12 1/4 
1/5 1/20 1/30 1/20 1/5

Time and Space Complexity Analyses

Time Complexity: O(n²)

The time complexity of this program is O(n²), where n is the number of rows in the Leibniz Harmonic Triangle. This is because the program generates the triangle by computing each entry as the sum of two previous entries, and there are n2 entries in the triangle.

Space Complexity: O(n²)

The space complexity of this program is also O(n²), because it stores the entire triangle in a 2-D vector of size (n + 1) * (n + 1).

Conclusion

In the above article, we discussed an approach to generate a leibniz harmonic triangle uptill a given number of rows. Leibniz Harmonic Triangle is an interesting mathematical concept that is similar to pascal triangle. The concept, implementation, solution approach along with the pseudocode, algorithm used and C++ program was discussed. We also analyzed the time and space complexity of our solution.