Kurtosis – Definition, Example, Types

Kurtosis is a statistical term used to quantify distribution that is like skewness. Unlike skewness, which only distinguishes absolute value in one tail from those in the other, kurtosis assesses extreme values in both tails. Tail data exceeds the tails of the normal distribution in distributions with strong kurtosis. The tails of ranges with low kurtosis are often less severe than the tails of a normal circulation.

A high kurtosis is a trend that investors watch closely as it could result that there will be sharper results in either directions of profits or loss. This in comparison to the normal deviation or the regular changes. Kurtosis risk is the name given to this indicator that gives investor a sign about their assets.

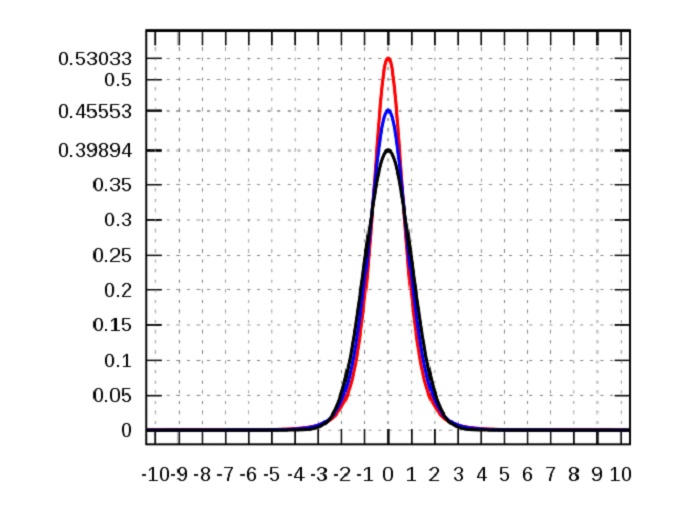
What is KURTOSIS?

The aggregate weight of a allotment's tails compared to the center of the distribution is measured by kurtosis. A bell peak is shown with most data within three standard deviations within + or - variations of the mean and can be seen when normal data is graphed using a histogram. During a strong kurtosis, this bell histogram tends to extend beyond the normal variations’ length.

In this statistical tool there is sometimes a case of confusion when distribution peak occurs. It must be remembered that Kurtosis is a graph of shape that gives an over all picture about distributions tail when compared to its complete shape.

With low kurtosis, a distribution can be extremely peaked as well, and with infinite kurtosis, it can be completely normal or flat with no deviation. Therefore, this tool calculates and focusses more on the “tailendness” instead of peak.

What are different types of Kurtosis?

The excess kurtosis of a given distribution determines the forms of kurtosis. Excess kurtosis can be either positive or negative, as well as near to zero.

• Mesokurtic - Excess Kurtosis

This type of pattern is typically recognized for its excess kurtosis of zero or close to zero is seen in data that followed a mesokurtic distribution. This suggests the data has a mesokurtic distribution if it follows a normal distribution.

• Leptokurtic – Positive Excess Kurtosis

A positively skewed kurtosis is indicated by the term leptokurtic. It is characterized by huge tails on either side with large outliers. For investors, this could mean that the result would be an extreme of positive or negative. Thus, this graph could indicate a risky pattern for investors to make investment on either side of the distribution.

• Platykurtic – Negative Excess Kurtosis

The excess kurtosis in a platykurtic distribution is negative that is characterized by a flat-tail distribution. The minor outliers in a distribution are indicated by the flat tails. The platykurtic distribution of investment returns is advantageous for investors in the financial context as this would mean a higher return on investment.