
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Javascript Program to Count Pairs with Given Sum
To count pairs with given sum, is a common problem asked in job interviews and is often used in many real-world applications such as cryptography and data compression.
In this article we are having an array and a target sum value, our task is to write a Javascript program to count pairs with given sum.
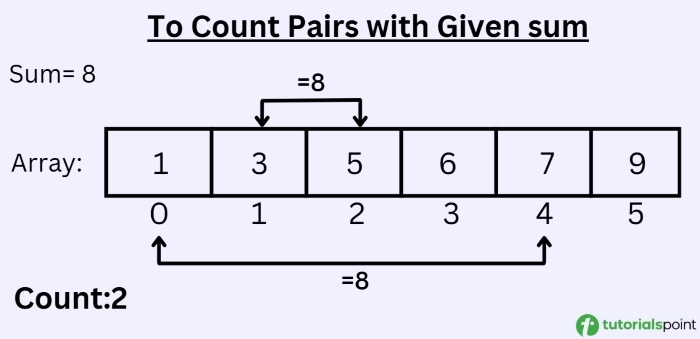
Example
Input: arr = [1, 2, 3, 5, 6, 7, 9] sum = 8 Pairs = (1, 7), (2,6), (3, 5) Output: Count: 3
Approaches to Count Pairs with Given Sum
Here is a list of approaches to count pairs with given sum in JavaScript which we will be discussing in this article with stepwise explanation and complete example codes.
Using Brute Force
To count pairs with given sum, we will be using brute force approach to iterate through all pairs of elements and check if their sum is equal to the given sum.
- First we have declared an array as arr and a sum value and defined a function countPair() that accepts array, and sum as its arguments.
- Then we have declared a counter variable which will keep count of pairs.
- Then we have used two for loop, where outer loop selects one element in each iteration and inner loop makes pairs of remaining element with selected element in outer loop.
- The if condition checks if pair sum is equal to target sum. If they are equal, it increment the counter by 1.
- After completing the loop, return the counter variable. The counter is displayed in web console using console.log() method.
Example
Here is a complete example code implementing above mentioned steps to count pairs with given sum in JavaScript using brute force technique.
let arr = [1, 2, 3, 5, 6, 7, 9], sum = 8;
function countPair(array, sum) {
let counter = 0;
for (i = 0; i < array.length; i++) {
for (j = i + 1; j < array.length; j++) {
if (array[i] + array[j] == sum) {
counter++;
}
}
}
return counter;
}
console.log("Number of pair with sum " +sum +" is: "
+countPair(arr, sum));
Using Two Pointers
In this approach to count pairs with given sum, we will be using two pointers technique.
- We have declared an array arr and a variable sum initially. We have defined a function countPair() that accepts the array and target sum value as its argument.
- We have sorted the array using sort() method, declared a count variable and currSum that stores the sum of pairs of element.
- Then we have defined two pointers, left and right where left pointer represents first element of the array and right pointer points to last element of the array.
- Then we find sum using left and right indices. If the currSum is equal to the target sum, then we increment the count variable by 1. We also increment the left pointer and decrement the right pointer by 1.
- If the currSum is less than the target sum, increment left and if the currSum is greater than the target sum, decrement right by 1. This loop continues till left pointer is less than right pointer using while loop.
- After completing the loop, return the count variable. The count is displayed in web console using console.log() method.
Example
Here is a complete example code implementing above mentioned steps to count pairs with given sum in JavaScript using two pointers technique.
let arr = [1, 2, 3, 5, 6, 7, 9], sum = 8;
function countPair(array, sum) {
array.sort((a, b) => a - b);
let left = 0;
let right = array.length - 1;
let count = 0;
while (left < right) {
const currSum = arr[left] + arr[right];
if (currSum === sum) {
count++;
left++;
right--;
} else if (currSum < sum) {
left++;
} else {
right--;
}
}
return count;
}
console.log("Number of pair with sum " +sum +" is: "
+countPair(arr, sum));
Using Hash Map
In this approach to count pairs with given sum, we will be using hash map. In this approach we make key-value pair of array elements with its frequency and check the complement of element with sum. If the complement exist then we increase the counter with the value corresponding to the array element/key.
- We have declared an array arr and a variable sum initially. We have defined a function countPair() that accepts the array and target sum value as its argument.
- Then we have declared hash_map and initialized it as an empty object to implement a hash map. We have used for loop to build our hash map. The if condition checks if arr[index] exist as key in the hash map or not.
- If keys doesn't exist, then it is initialized with 0 and if the key already exist then it's frequency is incremented by one.
- Then we have used next for loop to check if the complement of the current element exist in hash map using hash_map[sum - array[i]].
- If the complement exist then increase the count by 1. This process keeps repeating till we have checked the complement of each element. After the loop half of the count is returned. The count is displayed in web console using console.log() method.
Solution
Input:
array = [1, 2, 3, 4]
sum = 4
Building the hash map:
{1:1, 2:1, 3:1, 4:1}
Complement of elements in array:
for i = 0, array[0] = 1
sum - array[0] = 4-1 = 3
Since 3 exist with value 1 i.e hash_map[3] = 1
count = 1
for i = 1, array[1] = 2
sum - array[0] = 4-2 = 2
Since 2 exist with value 1 i.e hash_map[2] = 1
count = 2
for i = 2, array[2] = 3
sum - array[0] = 4-3 = 1
Since 1 exist with value 1 i.e hash_map[1] = 1
count = 3
for i = 3, array[3] = 4
sum - array[0] = 4-4 = 0
Since 0 does not exist, no increment
count = 3
=> Math.floor(count/2) = 1
Output:
Count: 1
Example
Here is a complete example code implementing above mentioned steps to count pairs with given sum in JavaScript using hash mapping technique.
let arr = [1, 2, 3, 5, 6, 7, 9], sum = 8;
function countPair(array, sum) {
let count = 0;
let hash_map = {};
for (let ind = 0; ind < array.length; ind++) {
if (!hash_map[array[ind]]) {
hash_map[array[ind]] = 0;
}
hash_map[arr[ind]]++;
}
for (let i = 0; i < array.length; i++) {
if (hash_map[sum - array[i]]) {
count += hash_map[sum - arr[i]];
}
}
return Math.floor(count / 2);
}
console.log("Number of pair with sum " +sum +" is: "
+countPair(arr, sum));
Complexity Comparison
Here is a comparison of time and space complexity of all the above approaches.
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(n^2) | O(1) |
| Two Pointer | O(nlog n) | O(1) (without sorting), O(n) (with sorting) |
| Hash Map | O(n) | O(n) |
Conclusion
In this article, Javascript program to count pairs with given sum, we have used three different approaches. These approaches are: by using brute force, two pointers technique and by using hash map. With each approach, we have improved code efficiency as it can be seen in above table.
Practice and learn from a wide range of JavaScript examples, including event handling, form validation, and advanced techniques. Interactive code snippets for hands-on learning.

