Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
hypot( ), hypotf( ), hypotl( ) in C++
In this article we will be discussing the working, syntax and examples of hypot( ), hypotf( ), hypotl( ) function in C++.
hypot( ) function
This function is used to compute the hypotenuse of a right angled triangle. This function returns the square root of sum of square of two variables. It is a function of <cmath> header file.
What is hypotenuse?
Hypotenuse is the longest side of the right angle triangle. Below is the graphical representation of a hypotenuse in a right angle triangle.
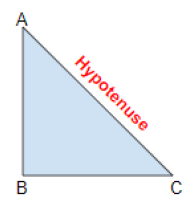
In above figure AC side of the triangle is a hypotenuse.
The formula to calculate hypotenuse is −
$$H = \sqrt{x^2+Y^2}$$
Syntax
Data type hypot(data type X, data type Y);
Parameters
The hypot( ) takes two or three parameters X, Y.
Example
Inputs: X=3 Y=4 Output: 5 Input: X=12 Y=5 Output: 13
Return value
The square root of (X2 + Y2)
Approach can be followed
First we initialize the two variables.
Then we define the hypot( ) function.
Then we print the square root.
By using above approach we can calculate the square root of sum of square of two variables. It is calculated by formula of h=sqrt(x2+y2).
Example
// c++ program to demonstrate the working of hypot( ) function
#include<cmath.h>
#include<iostream.h>
Using namespace std;
int main( ){
// initialize the two values
int a=3, b=4, c;
cout<< “ A= ”<< a << “B= ” << b;
// define the hypot( ) function
c = hypot(a, b);
cout << “C= “ <<c<<endl;
double x, y, z;
x=12;
y=5;
cout<< “X=”<<x<< “Y=”<<y;
z = hypot(x, y);
cout<< “Z= “<<z;
return 0;
}Output
If we run the above code then it will generate the following output
OUTPUT - A=3 B=4 C= 5 OUTPUT - X=12 Y=5 Z=13
hypotf( ) function
hypotf( ) function performs same task as hypot function. But difference is hypotf( ) function returns the float data type. And the parameter is also float type. It is a function of <cmath> header file.
Syntax
float hypotf(float x);
Example
Output – X= 9.34 Y=10.09 Z= 13.75 Output – X= 12.75 Y=5.56 Z= 13.90956
Approach can be followed
First we initialize the two variables in float data type.
Then we define the hypotf( ) function.
Then we print the square root.
By above we can calculate the square root.
Example
// c++ program to demonstrate the working of hypotf( ) function
#include<iostream.h>
#include<cmath.h>
Using namespace std;
int main( ){
float x = 12.75, y = 5.56, z;
cout<< “X= “<<x<< “Y= “ <<y;
z = hypotf(x, y);
cout << “Z= “<<z;
return 0;
}Output
If we run the above code then it will generate the following output
OUTPUT – X= 12.75 Y=5.56 Z=13.90956 OUTPUT – X=9.34 Y=10.09 Z= 13.75
hypotl( ) function
hypotl( ) function performs same task as the hypotl( ) function, but the difference is hypotl( ) function return the long double data type. And the parameter is also long double data type. It is function of <cmath > header file.
Syntax
Long double hypotl( long double z)
Example
Output – X= 9.34 Y=10.09 Z= 13.75 Output – X= 12.75 Y=5.56 Z= 13.90956
Approach can be followed
First we initialize the two variables in long double data type.
Then we define the hypotl( ) function.
Then we print the square root.
By above we can calculate the square root.
Example
// c++ program to demonstrate the working of hypotl( ) function
#include<iostream.h>
#include<cmath.h>
Using namespace std;
int main( ){
long double x = 9.342553435, y = 10.0987456456, z;
cout<< “X= “<<x<< “Y= “ <<y;
z = hypotl(x, y);
cout<< “Z= “<<z;
return 0;
}Output
If we run the above code then it will generate the following output
OUTPUT – X= 9.3425453435 Y=10.0987456456 Z=13.7575 OUTPUT – X= 12.5854555 Y=5.125984 Z= 184.6694021107363
136 Views
To Continue Learning Please Login