How to solve diamond problem using default methods in Java

Inheritance is a relation between two classes where one class inherits the properties of the other class. This relation can be defined using the extends keyword as −

public class A extends B{
}

The class which inherits the properties is known as sub class or, child class and the class whose properties are inherited is super class or, parent class.

In inheritance a copy of super class members is created in the sub class object. Therefore, using the sub class object you can access the members of the both classes.

Multiple inheritance is where one class inherits the properties of multiple classes. In other words, in multiple inheritance we can have one child class and n number of parent classes. Java does not support multiple inheritance (with classes).

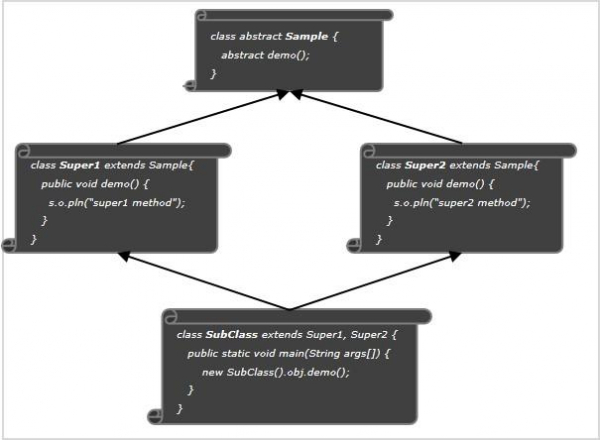
The diamond problem

• For instance, let us assume that Java does support multiple inheritance.
• And if we have an abstract class named Sample with an abstract method demo().
• Then if two other classes in the same package extends this class and try to implement its abstract method, demo().
• Then, as per the basic rule of inheritance, a copy of both demo() methods should be created in the subclass object which leaves the subclass with two methods with same prototype (name and arguments).
• Then, if you call the demo() method using the object of the subclass compiler faces an ambiguous situation not knowing which method to call. This issue is known as diamond problem in Java.

Solution to diamond problem

You can achieve multiple inheritance in Java, using the default methods (Java8) and interfaces.

From Java8 on wards default methods are introduced in an interface. Unlike other abstract methods these are the methods of an interface with a default implementation. If you have default method in an interface, it is not mandatory to override (provide body) it in the classes that are already implementing this interface.

You can have same default methods (same name and signature) in two different interfaces and, from a class you can implement these two interfaces.

If you do so, you must override the default method from the class explicitly specifying the default method along with its interface name.

Example

Live Demo

interface MyInterface1{  
   public static int num = 100;
   public default void display() {
      System.out.println("display method of MyInterface1");
   }
}
interface MyInterface2{  
   public static int num = 1000;
   public default void display() {
      System.out.println("display method of MyInterface2");
   }
}  
public class InterfaceExample implements MyInterface1, MyInterface2{
   public void display() {
      MyInterface1.super.display();
      //or,
      MyInterface2.super.display();
   }      
   public static void main(String args[]) {
      InterfaceExample obj = new InterfaceExample();
      obj.display();
   }
}

Output

display method of MyInterface1
display method of MyInterface2