
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How To Find Minimum Height of the Triangle with Given Base and Area in Java?
The height of a triangle is the perpendicular distance from a vertex to the line containing the opposite side (which is the base). The height is also known as altitude.
What is Minimum Height?
The minimum height of a triangle refers to the shortest possible altitude (perpendicular distance) from a vertex to the opposite side (base).
The following diagram provides you with a clear idea of the triangle's height and its base:
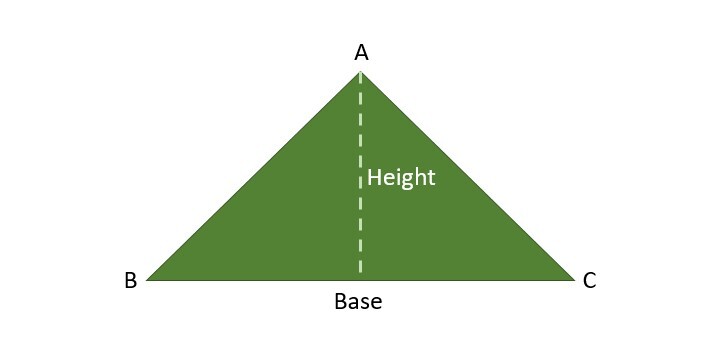
A triangle is a polygon (a basic shape in geometry) that has three sides and three corners. The corners, also called vertices, are zero-dimensional points, while the sides connecting them, also called edges, are one-dimensional line segments.
As the problem specifies, find the minimum height of the triangle with a given base and area. The area of a triangle is defined as the total region (amount of space) that is enclosed by the three sides of any particular triangle.
The triangle has a standard way to calculate its area:
area = 1/2 x base x height
If the area and base are given, we can easily find the minimum height of the triangle.
Example 1
In this example, we use the standard area formula to determine the minimum height (shortest altitude) of a triangle by using the given triangle area 6 and base 14:
public class findHeight {
public static void main(String args[]){
double area = 6;
System.out.println("The area of triangle: " + area);
double base = 14;
System.out.println("The base of triangle: " + base);
//find the height of the triangle using area and base
double height = (2 * area) / base;
System.out.println("The height of the triangle: " + height);
//Find minimum height of triangle by using ceil() method
double minHeight = Math.ceil(height);
System.out.println("The minimum height of the triangle: " + minHeight);
}
}
The above program produces the following output:
The area of triangle: 6.0 The base of triangle: 14.0 The height of the triangle: 0.8571428571428571 The minimum height of the triangle: 1.0
Example 2
In the example below, we define a method named findMinHeight() that takes two parameters, base and area. This method uses the standard area formula to calculate the minimum height of a triangle with a base of 6 and an area of 12:
public class findHeight {
// Define a method to calculate the min height
public static double findMinHeight(double base, double area) {
return (area * 2) / base;
}
public static void main(String[] args) {
double area = 12;
double base = 6;
System.out.println("The given area is: " + area);
System.out.println("The given base is: " + base);
//calling the findMinHeight() method to calculate minimum height
System.out.println("The minimum height of the triangle: " + findMinHeight(base, area));
}
}
Below is the output of the above program:
The area of a triangle: 12.0 The base of the triangle: 6.0 The minimum height of the triangle: 4.0

