Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How does the portfolio risk depend on the correlation between assets?
Portfolio Risk and Return
The general standard deviation (SD) of a portfolio is related to −
The weighted mean average of each individual variance, and
The generally weighted covariances between all assets in the portfolio of investment.
When a new asset is added to a large basket of portfolios with many assets, the new asset alters the portfolio's SD in two ways. It affects −
The new asset's own variance, and
The covariance between the new asset and each of the other assets in the portfolio.
The net effect of the numerous covariances will be more important than the effect of the asset's own variance. The more assets chosen and included in the portfolio, the more of this effect will be apparent.
Therefore, a new investment’s average covariance with all the other investments in the portfolio is more important than the new assets' own variance.
Including securities that are not perfectly positively correlated with each other will reduce the SD of the portfolio. The lower the correlations between two returns of assets in the portfolio, the lower the portfolio risk, and thus the higher the diversification benefits and vice versa.
Note − Most of the benefits of diversification occur when the net correlation between two assets is -1.00.
The following graph is for a portfolio with a net SD of zero, thus a risk-free portfolio. This occurs when two assets moving in opposite directions are combined.
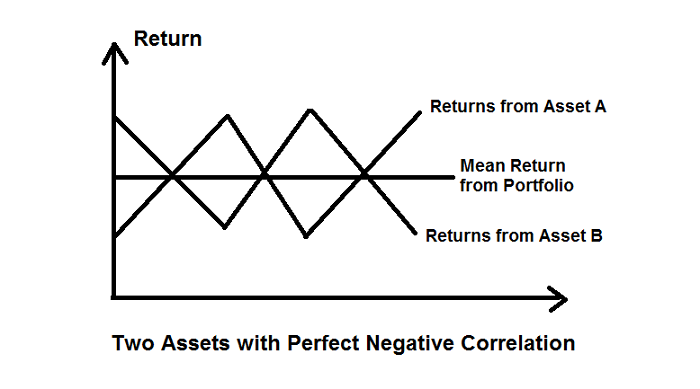
Returns on asset B move in the opposite direction from returns on asset A.
The middle-point between A and B shows the average mean return with no variability.
The average SD of this portfolio is zero.
This is an example of a risk-free portfolio.
In a two-asset portfolio, the ideal situation provides a palpable contrast in asset returns similar to the "sawtooth" diagram shown above. Thus, one asset usually completely offsets the other asset (in terms of risk) offering a smooth rate of return with no variability. However, for this, the two assets must have a perfect negative correlation.
$$\mathrm{σ_{Portfolio} =\sqrt{(π€_{π})^{2}(σ_{π})^{2} + (π€_{j})^{2}(σ_{j} )^{2}+ 2\:π€_{π}π€_{j}\:Cov_{π,π}}}$$
Therefore, the highest amount of risk reduction is determined by the correlation coefficient. The correlation coefficient drives the whole theory of portfolio diversification.
Example with Perfect Positive Correlation
What is the SD of a portfolio (E) assuming the following data?
- $σ_{1}$ = 0.1
- $π€_{1}$ = 0.5
- $σ_{2}$ = 0.1
- $π€_{2}$= 0.5
- $ρ_{12}$ = 1
Solution
$Cov_{12} = σ_{1} × ρ_{2} × ρ_{12} = 0.1 \times 0.1 \times 1 = 0.01$
Standard Deviation of Portfolio = 0.10 (perfect correlation)
Assuming there are three securities in the portfolio, the standard deviation is given by the following formula −
$$\mathrm{σ_{Portfolio} =\sqrt{(π€_{π})^{2}(σ_{π})^{2} + (π€_{j})^{2}(σ_{j})^{2}+ (π€_{k})^{2}(σ_{k})^{2} +2\:π€_{π}π€_{j}\:Cov_{π,π} + 2\:π€_{j}π€_{k}\:Cov_{π,π} + 2 \:π€_{k}π€_{π}\:Cov_{π,π}}}$$
2K+ Views
