Heptagonal number

A heptagonal number is a number which can be represented as a heptagon. A heptagon is a polygon with 7 sides. A heptagonal number can be represented as a combination of successive layers of heptagon( 7-sided polygon). Heptagonal number can be better explained with the below figures.

The first heptagonal number is 1. Thus, it can be represented by a single dot.

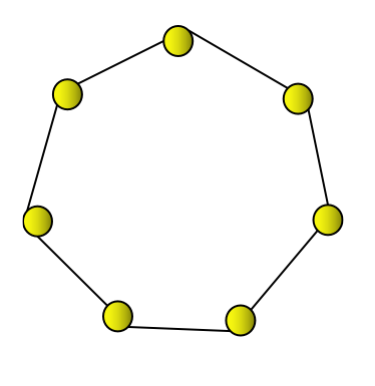
The second heptagonal number is 7 which can be represented by a heptagon.

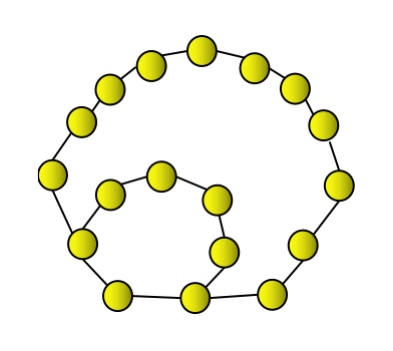
The third heptagonal number is 18 which can be represented as a heptagon and combined with a successive layer of heptagon.

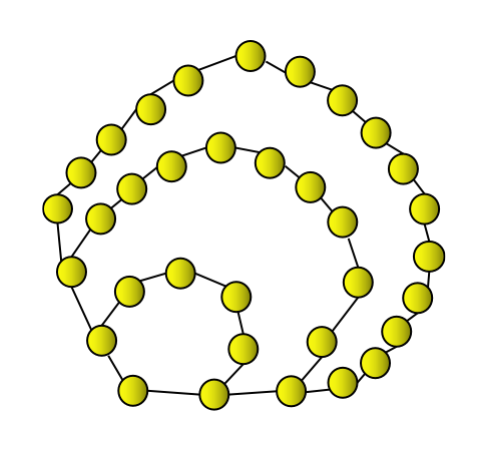
The fourth heptagonal number is 34. It can be represented as a heptagon combined with two successive heptagonal layers in the above shown manner which gives 34.

The similar concept will be used for further heptagonal numbers. With the same logic, the first few heptagonal numbers are 1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403……

Our task in this problem includes that we will be given any positive number N as an input and we need to print the Nth Heptagonal number as our output.

For example,

INPUT : N=6

OUTPUT : 81

INPUT : N=9

OUTPUT : 189

Now let’s look at the algorithm that we will use to solve this problem.

Algorithm

To solve this problem, we need to see the pattern that is being followed to calculate the nth heptagonal number. The nth heptagonal number can be represented as −

$$Heptagonal_{n}\:=\:\frac{n}{2}(5n\:-\:3)$$

If we closely observe the expression, every heptagonal number is of the form

$\frac{n}{2}(5n\:-\:3)$, where n represents the count of the heptagonal number.

Let's understand it better with examples.

For n=1,$\frac{1}{2}(5\:\times\:1\:-\:3)$= 1, which is the first heptagonal number.

For n=2,$\frac{2}{2}(5\:\times\:2\:-\:3)$= 7, which is the second heptagonal number.

For n=3,$\frac{3}{2}(5\:\times\:3\:-\:3)$= 18, which is the third heptagonal number.

Now, let's check it for n=8.$\frac{8}{2}(5\:\times\:8\:-\:3)$ gives 148 which is actually the eighth heptagonal number in the sequence of heptagonal numbers.

Since we can get any nth heptagonal number using the above expression, we will be using this expression to calculate the nth heptagonal number in our approach where n can be any positive number.

Approach

The step-by-step illustration of the approach we will be following −

• Take any positive number N as input to calculate the corresponding heptagonal number for the value N.

• Initialise a function to calculate the Nth heptagonal number.

• Use the expression mentioned in algorithm section i.e.$\frac{N}{2}(5N\:-\:3)$ to calculate the Nth heptagonal number and store it in any variable.

• Return the variable in which we store the value which will be the Nth heptagonal number corresponding to any positive value N.

Note − We will use float data type instead of int data type to avoid any errors due to decimal values while calculating the Nth heptagonal number using the above mentioned formula.

Example

The implementation of the approach in C++ −

#include <bits/stdc++.h>
#include <iostream>
using namespace std;

//function to calculate nth heptagonal number using formula n/2(5n-3)
float heptagonal(float N){
   float ans= (N/2)*((5*N) - 3); //to store nth heptagonal number
   return ans;
}
int main(){
   float N=5; //input
   float a=heptagonal(N); //store the answer in a variable
   N=13;
   float b=heptagonal(N);
   cout<<a<<endl<<b<<endl; //print the answer
   return 0;
}

Output

55
403

Time Complexity : O(1) , since constant time is taken.

Space Complexity : O(1) , since no extra space is taken.

Conclusion

We have tried to learn the concept of heptagonal number and the formula used to calculate the nth heptagonal number which we used in our approach.

I hope you find this article helpful to learn the concept of printing nth heptagonal number for any user input for n.