- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Graph Fundamentals
A graph is a diagram of points and lines connected to the points. It has at least one line joining a set of two vertices with no vertex connecting itself. The concept of graphs in graph theory stands up on some basic terms such as point, line, vertex, edge, degree of vertices, properties of graphs, etc. Here, in this chapter, we will cover these fundamentals of graph theory.
Point
A point is a particular position in a one-dimensional, two-dimensional, or three-dimensional space. For better understanding, a point can be denoted by an alphabet. It can be represented with a dot.
Example
Here, the dot is a point named ‘a’.
Line
A Line is a connection between two points. It can be represented with a solid line.
Example
Here, ‘a’ and ‘b’ are the points. The link between these two points is called a line.
Vertex
A vertex is a point where multiple lines meet. It is also called a node. Similar to points, a vertex is also denoted by an alphabet.
Example
Here, the vertex is named with an alphabet ‘a’.
Edge
An edge is the mathematical term for a line that connects two vertices. Many edges can be formed from a single vertex. Without a vertex, an edge cannot be formed. There must be a starting vertex and an ending vertex for an edge.
Example
Here, ‘a’ and ‘b’ are the two vertices and the link between them is called an edge.
Graph
A graph ‘G’ is defined as G = (V, E) Where V is a set of all vertices and E is a set of all edges in the graph.
Example 1
In the above example, ab, ac, cd, and bd are the edges of the graph. Similarly, a, b, c, and d are the vertices of the graph.
Example 2
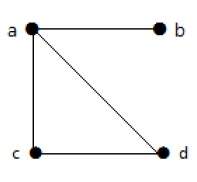
In this graph, there are four vertices a, b, c, and d, and four edges ab, ac, ad, and cd.
Loop
In a graph, if an edge is drawn from vertex to itself, it is called a loop.
Example 1
In the above graph, V is a vertex for which it has an edge (V, V) forming a loop.
Example 2
In this graph, there are two loops which are formed at vertex a, and vertex b.
357 Views
