Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Graph and its representations
The graph is a non-linear data structures. This represents data using nodes, and their relations using edges. A graph G has two sections. The vertices, and edges. Vertices are represented using set V, and Edges are represented as set E. So the graph notation is G(V,E). Let us see one example to get the idea.
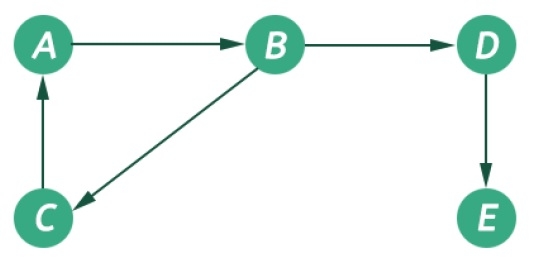
In this graph, there are five vertices and five edges. The edges are directed. As an example, if we choose the edge connecting vertices B and D, the source vertex is B and destination is D. So we can move B to D but not move from D to B.
The graphs are non-linear, and it has no regular structure. To represent a graph in memory, there are few different styles. These styles are −
- Adjacency matrix representation
- Edge list representation
- Adjacency List representation
Adjacency Matrix Representation
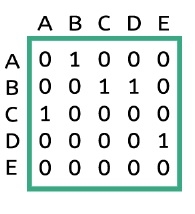
We can represent a graph using Adjacency matrix. The given matrix is an adjacency matrix. It is a binary, square matrix and from ith row to jth column, if there is an edge, that place is marked as 1. When we will try to represent an undirected graph using adjacency matrix, the matrix will be symmetric.
Edge List Representation
Graphs can be represented using one dimensional array also. This is called the edge list. In this representation there are five edges are present, for each edge the first element is the source and the second one is the destination. For undirected graph representation the number of elements in the edge list will be doubled.
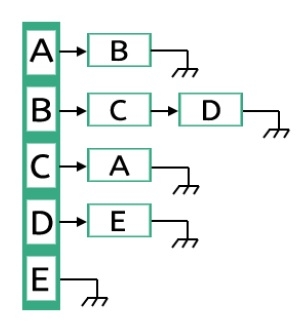
Adjacency List Representation
This is another type of graph representation. It is called the adjacency list. This representation is based on Linked Lists. In this approach, each Node is holding a list of Nodes, which are Directly connected with that vertices. At the end of list, each node is connected with the null values to tell that it is the end node of that list.
6K+ Views
