
- Genetic Algorithms – Home
- Genetic Algorithms – Introduction
- Genetic Algorithms – Fundamentals
- Genotype Representation
- Genetic Algorithms – Population
- Genetic Algorithms – Fitness Function
- Genetic Algorithms – Parent Selection
- Genetic Algorithms – Crossover
- Genetic Algorithms – Mutation
- Survivor Selection
- Termination Condition
- Models Of Lifetime Adaptation
- Effective Implementation
- Advanced Topics
- Application Areas
- Further Readings
Genetic Algorithms - Parent Selection
Parent Selection is the process of selecting parents which mate and recombine to create off-springs for the next generation. Parent selection is very crucial to the convergence rate of the GA as good parents drive individuals to a better and fitter solutions.
However, care should be taken to prevent one extremely fit solution from taking over the entire population in a few generations, as this leads to the solutions being close to one another in the solution space thereby leading to a loss of diversity. Maintaining good diversity in the population is extremely crucial for the success of a GA. This taking up of the entire population by one extremely fit solution is known as premature convergence and is an undesirable condition in a GA.
Fitness Proportionate Selection
Fitness Proportionate Selection is one of the most popular ways of parent selection. In this every individual can become a parent with a probability which is proportional to its fitness. Therefore, fitter individuals have a higher chance of mating and propagating their features to the next generation. Therefore, such a selection strategy applies a selection pressure to the more fit individuals in the population, evolving better individuals over time.
Consider a circular wheel. The wheel is divided into n pies, where n is the number of individuals in the population. Each individual gets a portion of the circle which is proportional to its fitness value.
Two implementations of fitness proportionate selection are possible −
Roulette Wheel Selection
In a roulette wheel selection, the circular wheel is divided as described before. A fixed point is chosen on the wheel circumference as shown and the wheel is rotated. The region of the wheel which comes in front of the fixed point is chosen as the parent. For the second parent, the same process is repeated.
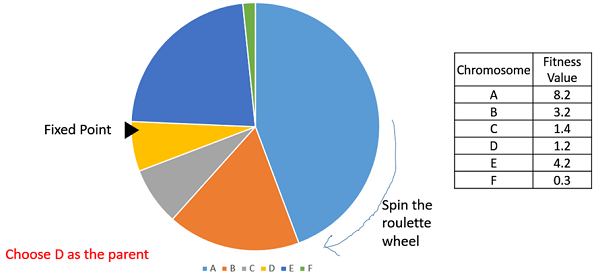
It is clear that a fitter individual has a greater pie on the wheel and therefore a greater chance of landing in front of the fixed point when the wheel is rotated. Therefore, the probability of choosing an individual depends directly on its fitness.
Implementation wise, we use the following steps −
Calculate S = the sum of a finesses.
Generate a random number between 0 and S.
Starting from the top of the population, keep adding the finesses to the partial sum P, till P<S.
The individual for which P exceeds S is the chosen individual.
Stochastic Universal Sampling (SUS)
Stochastic Universal Sampling is quite similar to Roulette wheel selection, however instead of having just one fixed point, we have multiple fixed points as shown in the following image. Therefore, all the parents are chosen in just one spin of the wheel. Also, such a setup encourages the highly fit individuals to be chosen at least once.
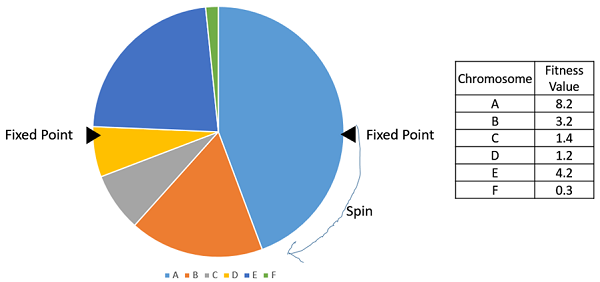
It is to be noted that fitness proportionate selection methods dont work for cases where the fitness can take a negative value.
Tournament Selection
In K-Way tournament selection, we select K individuals from the population at random and select the best out of these to become a parent. The same process is repeated for selecting the next parent. Tournament Selection is also extremely popular in literature as it can even work with negative fitness values.
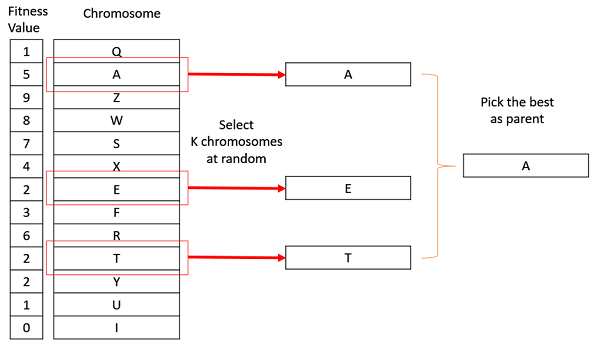
Rank Selection
Rank Selection also works with negative fitness values and is mostly used when the individuals in the population have very close fitness values (this happens usually at the end of the run). This leads to each individual having an almost equal share of the pie (like in case of fitness proportionate selection) as shown in the following image and hence each individual no matter how fit relative to each other has an approximately same probability of getting selected as a parent. This in turn leads to a loss in the selection pressure towards fitter individuals, making the GA to make poor parent selections in such situations.
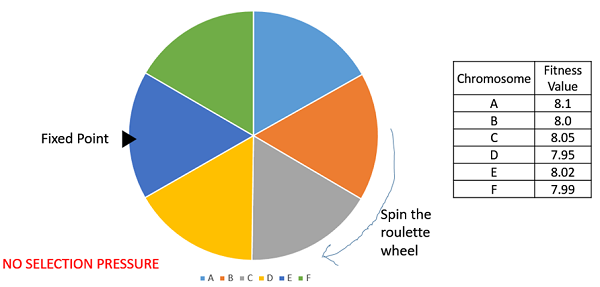
In this, we remove the concept of a fitness value while selecting a parent. However, every individual in the population is ranked according to their fitness. The selection of the parents depends on the rank of each individual and not the fitness. The higher ranked individuals are preferred more than the lower ranked ones.
| Chromosome | Fitness Value | Rank |
|---|---|---|
| A | 8.1 | 1 |
| B | 8.0 | 4 |
| C | 8.05 | 2 |
| D | 7.95 | 6 |
| E | 8.02 | 3 |
| F | 7.99 | 5 |
Random Selection
In this strategy we randomly select parents from the existing population. There is no selection pressure towards fitter individuals and therefore this strategy is usually avoided.