Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Frog Position After T Seconds in C++
Suppose we have one undirected tree consisting of n vertices. The vertices are numbered from 1 to n. Now a frog starts jumping from the vertex 1. The frog can jump from its current vertex to another non-visited vertex if they are adjacent, in one second. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them
where the probability is same, otherwise, when the frog can not jump to any non-visited vertex it jumps forever on the same vertex.
The tree is given as an array of edges. We have to find the probability that after t seconds the frog is on the vertex target.
So, if the input is like n is 7, t is 2, target is 4 and the tree is like −
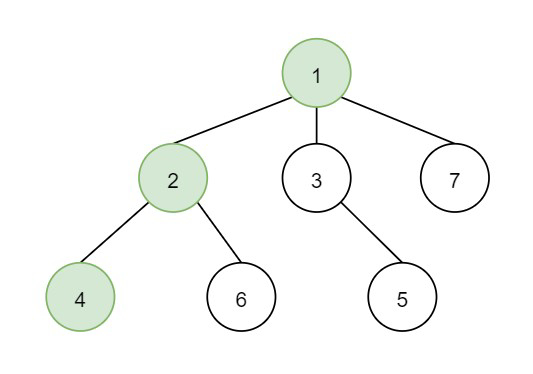
then the output will be 0.1666, as from the graph. The frog starts at vertex 1, jumping with 0.3333 probability to the vertex 2 after second 1 and then jumping with 0.5 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 0.3333 * 0.5 = 1.6665.
To solve this, we will follow these steps −
ret := 1
Define one set visited
Define a function dfs(), this will take node, start, a list of edges g, time, t, one stack st,
if node is member of visited, then −
return false
insert node into visited
if node is same as 1, then −
tt := time, ok := true
return true
for initialize i := 0, when i < size of g[node], update (increase i by 1), do −
insert g[node, i] into st
if dfs(g[node, i], start, g, time + 1, t, st) is true, then −
return true
delete element from st
return false
From the main method do the following −
ret := 1
ok := false
Define an array of lists graph of size n + 1
Define an array of lists graph2 of size n + 1
for initialize i := 0, when i < size of edges, update (increase i by 1), do −
insert edges[i, 1] at the end of graph[edges[i, 0]]
insert edges[i, 0] at the end of graph[edges[i, 1]]
Define one stack st
dfs(target, target, graph, 0, t, st)
while (not st is empty), do −
node := top element of st
sz := size of graph[node]
if node is not equal to 1, then −
(decrease sz by 1)
ret := ret * (1.0 / sz)
delete element from st
if tt > t, then −
return 0
if tt is same as t, then −
return ret
if tt < t and target is same as 1 and size of graph[target] >= 1, then −
return 0
return (if tt < t and size of graph[target] > 1, then 0, otherwise ret)
Let us see the following implementation to get better understanding −
Example
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
double ret = 1;
bool ok;
set<int> visited;
int tt;
bool dfs(int node, int start, vector<int> g[], int time, int t,
stack<int>& st){
if (visited.count(node))
return false;
visited.insert(node);
if (node == 1) {
tt = time;
ok = true;
return true;
}
for (int i = 0; i < g[node].size(); i++) {
st.push(g[node][i]);
if (dfs(g[node][i], start, g, time + 1, t, st))
return true;
;
st.pop();
}
return false;
}
double frogPosition(int n, vector<vector<int> >& edges, int t,
int target){
ret = 1;
ok = false;
vector<int> graph[n + 1];
vector<int> graph2[n + 1];
for (int i = 0; i < edges.size(); i++) {
graph[edges[i][0]].push_back(edges[i][1]);
graph[edges[i][1]].push_back(edges[i][0]);
}
stack<int> st;
dfs(target, target, graph, 0, t, st);
while (!st.empty()) {
int node = st.top();
double sz = (double)graph[node].size();
if (node != 1)
sz--;
ret *= (1.0 / sz);
st.pop();
}
if (tt > t)
return 0;
if (tt == t)
return ret;
if (tt < t && target == 1 && graph[target].size() >= 1)
return 0;
return tt < t && graph[target].size() > 1 ? 0 : ret;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{1,2},{1,3},{1,7},{2,4},{2,6},{3,5}};
cout << (ob.frogPosition(7,v,2,4));
}Input
7, {{1,2},{1,3},{1,7},{2,4},{2,6},{3,5}}, 2, 4Output
0.166667
206 Views
