
- Fortran - Home
- Fortran - Overview
- Fortran - Environment Setup
- Fortran - Basic Syntax
- Fortran - Data Types
- Fortran - Variables
- Fortran - Constants
- Fortran - Operators
- Fortran - Decisions
- Fortran - Loops
- Fortran - Numbers
- Fortran - Characters
- Fortran - Strings
- Fortran - Arrays
- Fortran - Dynamic Arrays
- Fortran - Derived Data Types
- Fortran - Pointers
- Fortran - Basic Input Output
- Fortran - File Input Output
- Fortran - Procedures
- Fortran - Modules
- Fortran - Intrinsic Functions
- Fortran - Numeric Precision
- Fortran - Program Libraries
- Fortran - Programming Style
- Fortran - Debugging Program
Fortran - Quick Guide
Fortran - Overview
Fortran, as derived from Formula Translating System, is a general-purpose, imperative programming language. It is used for numeric and scientific computing.
Fortran was originally developed by IBM in the 1950s for scientific and engineering applications. Fortran ruled this programming area for a long time and became very popular for high performance computing, because.
It supports −
- Numerical analysis and scientific computation
- Structured programming
- Array programming
- Modular programming
- Generic programming
- High performance computing on supercomputers
- Object oriented programming
- Concurrent programming
- Reasonable degree of portability between computer systems
Facts about Fortran
Fortran was created by a team, led by John Backus at IBM in 1957.
Initially the name used to be written in all capital, but current standards and implementations only require the first letter to be capital.
Fortran stands for FORmula TRANslator.
Originally developed for scientific calculations, it had very limited support for character strings and other structures needed for general purpose programming.
Later extensions and developments made it into a high level programming language with good degree of portability.
Original versions, Fortran I, II and III are considered obsolete now.
Oldest version still in use is Fortran IV, and Fortran 66.
Most commonly used versions today are : Fortran 77, Fortran 90, and Fortran 95.
Fortran 77 added strings as a distinct type.
Fortran 90 added various sorts of threading, and direct array processing.
Fortran - Environment Setup
Setting up Fortran in Windows
G95 is the GNU Fortran multi-architechtural compiler, used for setting up Fortran in Windows. The windows version emulates a unix environment using MingW under windows. The installer takes care of this and automatically adds g95 to the windows PATH variable.
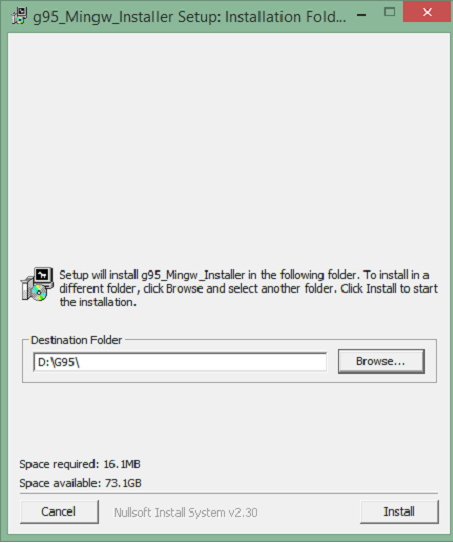
How to use G95
During installation, g95 is automatically added to your PATH variable if you select the option RECOMMENDED. This means that you can simply open a new Command Prompt window and type g95 to bring up the compiler. Find some basic commands below to get you started.
| Sr.No | Command & Description |
|---|---|
| 1 |
g95 c hello.f90 Compiles hello.f90 to an object file named hello.o |
| 2 |
g95 hello.f90 Compiles hello.f90 and links it to produce an executable a.out |
| 3 |
g95 -c h1.f90 h2.f90 h3.f90 Compiles multiple source files. If all goes well, object files h1.o, h2.o and h3.o are created |
| 4 |
g95 -o hello h1.f90 h2.f90 h3.f90 Compiles multiple source files and links them together to an executable file named 'hello' |
Command line options for G95
-c Compile only, do not run the linker. -o Specify the name of the output file, either an object file or the executable.
Multiple source and object files can be specified at once. Fortran files are indicated by names ending in ".f", ".F", ".for", ".FOR", ".f90", ".F90", ".f95", ".F95", ".f03" and ".F03". Multiple source files can be specified. Object files can be specified as well and will be linked to form an executable file.
Fortran - Basic Syntax
A Fortran program is made of a collection of program units like a main program, modules, and external subprograms or procedures.
Each program contains one main program and may or may not contain other program units. The syntax of the main program is as follows −
program program_name implicit none ! type declaration statements ! executable statements end program program_name
A Simple Program in Fortran
Lets write a program that adds two numbers and prints the result −
program addNumbers ! This simple program adds two numbers implicit none ! Type declarations real :: a, b, result ! Executable statements a = 12.0 b = 15.0 result = a + b print *, 'The total is ', result end program addNumbers
When you compile and execute the above program, it produces the following result −
The total is 27.0000000
Please note that −
All Fortran programs start with the keyword program and end with the keyword end program, followed by the name of the program.
The implicit none statement allows the compiler to check that all your variable types are declared properly. You must always use implicit none at the start of every program.
Comments in Fortran are started with the exclamation mark (!), as all characters after this (except in a character string) are ignored by the compiler.
The print * command displays data on the screen.
Indentation of code lines is a good practice for keeping a program readable.
Fortran allows both uppercase and lowercase letters. Fortran is case-insensitive, except for string literals.
Basics
The basic character set of Fortran contains −
- the letters A ... Z and a ... z
- the digits 0 ... 9
- the underscore (_) character
- the special characters = : + blank - * / ( ) [ ] , . $ ' ! " % & ; < > ?
Tokens are made of characters in the basic character set. A token could be a keyword, an identifier, a constant, a string literal, or a symbol.
Program statements are made of tokens.
Identifier
An identifier is a name used to identify a variable, procedure, or any other user-defined item. A name in Fortran must follow the following rules −
It cannot be longer than 31 characters.
It must be composed of alphanumeric characters (all the letters of the alphabet, and the digits 0 to 9) and underscores (_).
First character of a name must be a letter.
Names are case-insensitive
Keywords
Keywords are special words, reserved for the language. These reserved words cannot be used as identifiers or names.
The following table, lists the Fortran keywords −
| The non-I/O keywords | ||||
|---|---|---|---|---|
| allocatable | allocate | assign | assignment | block data |
| call | case | character | common | complex |
| contains | continue | cycle | data | deallocate |
| default | do | double precision | else | else if |
| elsewhere | end block data | end do | end function | end if |
| end interface | end module | end program | end select | end subroutine |
| end type | end where | entry | equivalence | exit |
| external | function | go to | if | implicit |
| in | inout | integer | intent | interface |
| intrinsic | kind | len | logical | module |
| namelist | nullify | only | operator | optional |
| out | parameter | pause | pointer | private |
| program | public | real | recursive | result |
| return | save | select case | stop | subroutine |
| target | then | type | type() | use |
| Where | While | |||
| The I/O related keywords | ||||
| backspace | close | endfile | format | inquire |
| open | read | rewind | Write | |
Fortran - Data Types
Fortran provides five intrinsic data types, however, you can derive your own data types as well. The five intrinsic types are −
- Integer type
- Real type
- Complex type
- Logical type
- Character type
Integer Type
The integer types can hold only integer values. The following example extracts the largest value that can be held in a usual four byte integer −
program testingInt implicit none integer :: largeval print *, huge(largeval) end program testingInt
When you compile and execute the above program it produces the following result −
2147483647
Note that the huge() function gives the largest number that can be held by the specific integer data type. You can also specify the number of bytes using the kind specifier. The following example demonstrates this −
program testingInt
implicit none
!two byte integer
integer(kind = 2) :: shortval
!four byte integer
integer(kind = 4) :: longval
!eight byte integer
integer(kind = 8) :: verylongval
!sixteen byte integer
integer(kind = 16) :: veryverylongval
!default integer
integer :: defval
print *, huge(shortval)
print *, huge(longval)
print *, huge(verylongval)
print *, huge(veryverylongval)
print *, huge(defval)
end program testingInt
When you compile and execute the above program, it produces the following result −
32767 2147483647 9223372036854775807 170141183460469231731687303715884105727 2147483647
Real Type
It stores the floating point numbers, such as 2.0, 3.1415, -100.876, etc.
Traditionally there are two different real types, the default real type and double precision type.
However, Fortran 90/95 provides more control over the precision of real and integer data types through the kind specifier, which we will study in the chapter on Numbers.
The following example shows the use of real data type −
program division implicit none ! Define real variables real :: p, q, realRes ! Define integer variables integer :: i, j, intRes ! Assigning values p = 2.0 q = 3.0 i = 2 j = 3 ! floating point division realRes = p/q intRes = i/j print *, realRes print *, intRes end program division
When you compile and execute the above program it produces the following result −
0.666666687 0
Complex Type
This is used for storing complex numbers. A complex number has two parts, the real part and the imaginary part. Two consecutive numeric storage units store these two parts.
For example, the complex number (3.0, -5.0) is equal to 3.0 5.0i
We will discuss Complex types in more detail, in the Numbers chapter.
Logical Type
There are only two logical values: .true. and .false.
Character Type
The character type stores characters and strings. The length of the string can be specified by len specifier. If no length is specified, it is 1.
For example,
character (len = 40) :: name name = Zara Ali
The expression, name(1:4) would give the substring Zara.
Implicit Typing
Older versions of Fortran allowed a feature called implicit typing, i.e., you do not have to declare the variables before use. If a variable is not declared, then the first letter of its name will determine its type.
Variable names starting with i, j, k, l, m, or n, are considered to be for integer variable and others are real variables. However, you must declare all the variables as it is good programming practice. For that you start your program with the statement −
implicit none
This statement turns off implicit typing.
Fortran - Variables
A variable is nothing but a name given to a storage area that our programs can manipulate. Each variable should have a specific type, which determines the size and layout of the variable's memory; the range of values that can be stored within that memory; and the set of operations that can be applied to the variable.
The name of a variable can be composed of letters, digits, and the underscore character. A name in Fortran must follow the following rules −
It cannot be longer than 31 characters.
It must be composed of alphanumeric characters (all the letters of the alphabet, and the digits 0 to 9) and underscores (_).
First character of a name must be a letter.
Names are case-insensitive.
Based on the basic types explained in previous chapter, following are the variable types −
| Sr.No | Type & Description |
|---|---|
| 1 |
Integer It can hold only integer values. |
| 2 |
Real It stores the floating point numbers. |
| 3 |
Complex It is used for storing complex numbers. |
| 4 |
Logical It stores logical Boolean values. |
| 5 |
Character It stores characters or strings. |
Variable Declaration
Variables are declared at the beginning of a program (or subprogram) in a type declaration statement.
Syntax for variable declaration is as follows −
type-specifier :: variable_name
For example
integer :: total real :: average complex :: cx logical :: done character(len = 80) :: message ! a string of 80 characters
Later you can assign values to these variables, like,
total = 20000 average = 1666.67 done = .true. message = A big Hello from Tutorials Point cx = (3.0, 5.0) ! cx = 3.0 + 5.0i
You can also use the intrinsic function cmplx, to assign values to a complex variable −
cx = cmplx (1.0/2.0, -7.0) ! cx = 0.5 7.0i cx = cmplx (x, y) ! cx = x + yi
Example
The following example demonstrates variable declaration, assignment and display on screen −
program variableTesting implicit none ! declaring variables integer :: total real :: average complex :: cx logical :: done character(len=80) :: message ! a string of 80 characters !assigning values total = 20000 average = 1666.67 done = .true. message = "A big Hello from Tutorials Point" cx = (3.0, 5.0) ! cx = 3.0 + 5.0i Print *, total Print *, average Print *, cx Print *, done Print *, message end program variableTesting
When the above code is compiled and executed, it produces the following result −
20000 1666.67004 (3.00000000, 5.00000000 ) T A big Hello from Tutorials Point
Fortran - Constants
The constants refer to the fixed values that the program cannot alter during its execution. These fixed values are also called literals.
Constants can be of any of the basic data types like an integer constant, a floating constant, a character constant, a complex constant, or a string literal. There are only two logical constants : .true. and .false.
The constants are treated just like regular variables, except that their values cannot be modified after their definition.
Named Constants and Literals
There are two types of constants −
- Literal constants
- Named constants
A literal constant have a value, but no name.
For example, following are the literal constants −
| Type | Example |
|---|---|
| Integer constants | 0 1 -1 300 123456789 |
| Real constants | 0.0 1.0 -1.0 123.456 7.1E+10 -52.715E-30 |
| Complex constants | (0.0, 0.0) (-123.456E+30, 987.654E-29) |
| Logical constants | .true. .false. |
| Character constants |
"PQR" "a" "123'abc$%#@!" " a quote "" " 'PQR' 'a' '123"abc$%#@!' ' an apostrophe '' ' |
A named constant has a value as well as a name.
Named constants should be declared at the beginning of a program or procedure, just like a variable type declaration, indicating its name and type. Named constants are declared with the parameter attribute. For example,
real, parameter :: pi = 3.1415927
Example
The following program calculates the displacement due to vertical motion under gravity.
program gravitationalDisp ! this program calculates vertical motion under gravity implicit none ! gravitational acceleration real, parameter :: g = 9.81 ! variable declaration real :: s ! displacement real :: t ! time real :: u ! initial speed ! assigning values t = 5.0 u = 50 ! displacement s = u * t - g * (t**2) / 2 ! output print *, "Time = ", t print *, 'Displacement = ',s end program gravitationalDisp
When the above code is compiled and executed, it produces the following result −
Time = 5.00000000 Displacement = 127.374992
Fortran - Operators
An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations. Fortran provides the following types of operators −
- Arithmetic Operators
- Relational Operators
- Logical Operators
Let us look at all these types of operators one by one.
Arithmetic Operators
Following table shows all the arithmetic operators supported by Fortran. Assume variable A holds 5 and variable B holds 3 then −
| Operator | Description | Example |
|---|---|---|
| + | Addition Operator, adds two operands. | A + B will give 8 |
| - | Subtraction Operator, subtracts second operand from the first. | A - B will give 2 |
| * | Multiplication Operator, multiplies both operands. | A * B will give 15 |
| / | Division Operator, divides numerator by de-numerator. | A / B will give 1 |
| ** | Exponentiation Operator, raises one operand to the power of the other. | A ** B will give 125 |
Relational Operators
Following table shows all the relational operators supported by Fortran. Assume variable A holds 10 and variable B holds 20, then −
| Operator | Equivalent | Description | Example |
|---|---|---|---|
| == | .eq. | Checks if the values of two operands are equal or not, if yes then condition becomes true. | (A == B) is not true. |
| /= | .ne. | Checks if the values of two operands are equal or not, if values are not equal then condition becomes true. | (A != B) is true. |
| > | .gt. | Checks if the value of left operand is greater than the value of right operand, if yes then condition becomes true. | (A > B) is not true. |
| < | .lt. | Checks if the value of left operand is less than the value of right operand, if yes then condition becomes true. | (A < B) is true. |
| >= | .ge. | Checks if the value of left operand is greater than or equal to the value of right operand, if yes then condition becomes true. | (A >= B) is not true. |
| <= | .le. | Checks if the value of left operand is less than or equal to the value of right operand, if yes then condition becomes true. | (A <= B) is true. |
Logical Operators
Logical operators in Fortran work only on logical values .true. and .false.
The following table shows all the logical operators supported by Fortran. Assume variable A holds .true. and variable B holds .false. , then −
| Operator | Description | Example |
|---|---|---|
| .and. | Called Logical AND operator. If both the operands are non-zero, then condition becomes true. | (A .and. B) is false. |
| .or. | Called Logical OR Operator. If any of the two operands is non-zero, then condition becomes true. | (A .or. B) is true. |
| .not. | Called Logical NOT Operator. Use to reverses the logical state of its operand. If a condition is true then Logical NOT operator will make false. | !(A .and. B) is true. |
| .eqv. | Called Logical EQUIVALENT Operator. Used to check equivalence of two logical values. | (A .eqv. B) is false. |
| .neqv. | Called Logical NON-EQUIVALENT Operator. Used to check non-equivalence of two logical values. | (A .neqv. B) is true. |
Operators Precedence in Fortran
Operator precedence determines the grouping of terms in an expression. This affects how an expression is evaluated. Certain operators have higher precedence than others; for example, the multiplication operator has higher precedence than the addition operator.
For example, x = 7 + 3 * 2; here, x is assigned 13, not 20 because operator * has higher precedence than +, so it first gets multiplied with 3*2 and then adds into 7.
Here, operators with the highest precedence appear at the top of the table, those with the lowest appear at the bottom. Within an expression, higher precedence operators will be evaluated first.
| Category | Operator | Associativity |
|---|---|---|
| Logical NOT and negative sign | .not. (-) | Left to right |
| Exponentiation | ** | Left to right |
| Multiplicative | * / | Left to right |
| Additive | + - | Left to right |
| Relational | < <= > >= | Left to right |
| Equality | == /= | Left to right |
| Logical AND | .and. | Left to right |
| Logical OR | .or. | Left to right |
| Assignment | = | Right to left |
Fortran - Decisions
Decision making structures require that the programmer specify one or more conditions to be evaluated or tested by the program, along with a statement or statements to be executed, if the condition is determined to be true, and optionally, other statements to be executed if the condition is determined to be false.
Following is the general form of a typical decision making structure found in most of the programming languages −
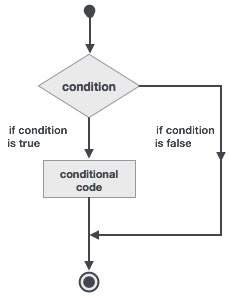
Fortran provides the following types of decision making constructs.
| Sr.No | Statement & Description |
|---|---|
| 1 |
If then construct
Anif then end if statementconsists of a logical expression followed by one or more statements. |
| 2 |
If then...else construct
Anif then statementcan be followed by an optionalelse statement, which executes when the logical expression is false. |
| 3 |
if...else if...else Statement
An if statement construct can have one or more optional else-if constructs. When the if condition fails, the immediately followed else-if is executed. When the else-if also fails, its successor else-if statement (if any) is executed, and so on. |
| 4 |
nested if construct
You can use oneiforelse ifstatement inside anotheriforelse ifstatement(s). |
| 5 |
select case construct
Aselect casestatement allows a variable to be tested for equality against a list of values. |
| 6 |
nested select case construct
You can use oneselect casestatement inside anotherselect case statement(s). |
Fortran - Loops
There may be a situation, when you need to execute a block of code several number of times. In general, statements are executed sequentially : The first statement in a function is executed first, followed by the second, and so on.
Programming languages provide various control structures that allow for more complicated execution paths.
A loop statement allows us to execute a statement or group of statements multiple times and following is the general form of a loop statement in most of the programming languages −
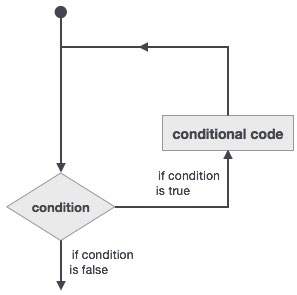
Fortran provides the following types of loop constructs to handle looping requirements. Click the following links to check their detail.
| Sr.No | Loop Type & Description |
|---|---|
| 1 |
do loop
This construct enables a statement, or a series of statements, to be carried out iteratively, while a given condition is true. |
| 2 |
do while loop
Repeats a statement or group of statements while a given condition is true. It tests the condition before executing the loop body. |
| 3 |
nested loops
You can use one or more loop construct inside any other loop construct. |
Loop Control Statements
Loop control statements change execution from its normal sequence. When execution leaves a scope, all automatic objects that were created in that scope are destroyed.
Fortran supports the following control statements. Click the following links to check their detail.
| Sr.No | Control Statement & Description |
|---|---|
| 1 |
exit
If the exit statement is executed, the loop is exited, and the execution of the program continues at the first executable statement after the end do statement. |
| 2 |
cycle
If a cycle statement is executed, the program continues at the start of the next iteration. |
| 3 |
stop
If you wish execution of your program to stop, you can insert a stop statement |
Fortran - Numbers
Numbers in Fortran are represented by three intrinsic data types −
- Integer type
- Real type
- Complex type
Integer Type
The integer types can hold only integer values. The following example extracts the largest value that could be hold in a usual four byte integer −
program testingInt implicit none integer :: largeval print *, huge(largeval) end program testingInt
When you compile and execute the above program it produces the following result −
2147483647
Please note that the huge() function gives the largest number that can be held by the specific integer data type. You can also specify the number of bytes using the kind specifier. The following example demonstrates this −
program testingInt
implicit none
!two byte integer
integer(kind = 2) :: shortval
!four byte integer
integer(kind = 4) :: longval
!eight byte integer
integer(kind = 8) :: verylongval
!sixteen byte integer
integer(kind = 16) :: veryverylongval
!default integer
integer :: defval
print *, huge(shortval)
print *, huge(longval)
print *, huge(verylongval)
print *, huge(veryverylongval)
print *, huge(defval)
end program testingInt
When you compile and execute the above program it produces the following result −
32767 2147483647 9223372036854775807 170141183460469231731687303715884105727 2147483647
Real Type
It stores the floating point numbers, such as 2.0, 3.1415, -100.876, etc.
Traditionally there were two different real types : the default real type and double precision type.
However, Fortran 90/95 provides more control over the precision of real and integer data types through the kind specifier, which we will study shortly.
The following example shows the use of real data type −
program division implicit none ! Define real variables real :: p, q, realRes ! Define integer variables integer :: i, j, intRes ! Assigning values p = 2.0 q = 3.0 i = 2 j = 3 ! floating point division realRes = p/q intRes = i/j print *, realRes print *, intRes end program division
When you compile and execute the above program it produces the following result −
0.666666687 0
Complex Type
This is used for storing complex numbers. A complex number has two parts : the real part and the imaginary part. Two consecutive numeric storage units store these two parts.
For example, the complex number (3.0, -5.0) is equal to 3.0 5.0i
The generic function cmplx() creates a complex number. It produces a result whos real and imaginary parts are single precision, irrespective of the type of the input arguments.
program createComplex implicit none integer :: i = 10 real :: x = 5.17 print *, cmplx(i, x) end program createComplex
When you compile and execute the above program it produces the following result −
(10.0000000, 5.17000008)
The following program demonstrates complex number arithmetic −
program ComplexArithmatic implicit none complex, parameter :: i = (0, 1) ! sqrt(-1) complex :: x, y, z x = (7, 8); y = (5, -7) write(*,*) i * x * y z = x + y print *, "z = x + y = ", z z = x - y print *, "z = x - y = ", z z = x * y print *, "z = x * y = ", z z = x / y print *, "z = x / y = ", z end program ComplexArithmatic
When you compile and execute the above program it produces the following result −
(9.00000000, 91.0000000) z = x + y = (12.0000000, 1.00000000) z = x - y = (2.00000000, 15.0000000) z = x * y = (91.0000000, -9.00000000) z = x / y = (-0.283783793, 1.20270276)
The Range, Precision and Size of Numbers
The range on integer numbers, the precision and the size of floating point numbers depends on the number of bits allocated to the specific data type.
The following table displays the number of bits and range for integers −
| Number of bits | Maximum value | Reason |
|---|---|---|
| 64 | 9,223,372,036,854,774,807 | (2**63)1 |
| 32 | 2,147,483,647 | (2**31)1 |
The following table displays the number of bits, smallest and largest value, and the precision for real numbers.
| Number of bits | Largest value | Smallest value | Precision |
|---|---|---|---|
| 64 | 0.8E+308 | 0.5E308 | 1518 |
| 32 | 1.7E+38 | 0.3E38 | 6-9 |
The following examples demonstrate this −
program rangePrecision implicit none real:: x, y, z x = 1.5e+40 y = 3.73e+40 z = x * y print *, z end program rangePrecision
When you compile and execute the above program it produces the following result −
x = 1.5e+40
1
Error : Real constant overflows its kind at (1)
main.f95:5.12:
y = 3.73e+40
1
Error : Real constant overflows its kind at (1)
Now let us use a smaller number −
program rangePrecision implicit none real:: x, y, z x = 1.5e+20 y = 3.73e+20 z = x * y print *, z z = x/y print *, z end program rangePrecision
When you compile and execute the above program it produces the following result −
Infinity 0.402144760
Now lets watch underflow −
program rangePrecision implicit none real:: x, y, z x = 1.5e-30 y = 3.73e-60 z = x * y print *, z z = x/y print *, z end program rangePrecision
When you compile and execute the above program it produces the following result −
y = 3.73e-60
1
Warning : Real constant underflows its kind at (1)
Executing the program....
$demo
0.00000000E+00
Infinity
The Kind Specifier
In scientific programming, one often needs to know the range and precision of data of the hardware platform on which the work is being done.
The intrinsic function kind() allows you to query the details of the hardwares data representations before running a program.
program kindCheck implicit none integer :: i real :: r complex :: cp print *,' Integer ', kind(i) print *,' Real ', kind(r) print *,' Complex ', kind(cp) end program kindCheck
When you compile and execute the above program it produces the following result −
Integer 4 Real 4 Complex 4
You can also check the kind of all data types −
program checkKind implicit none integer :: i real :: r character :: c logical :: lg complex :: cp print *,' Integer ', kind(i) print *,' Real ', kind(r) print *,' Complex ', kind(cp) print *,' Character ', kind(c) print *,' Logical ', kind(lg) end program checkKind
When you compile and execute the above program it produces the following result −
Integer 4 Real 4 Complex 4 Character 1 Logical 4
Fortran - Characters
The Fortran language can treat characters as single character or contiguous strings.
Characters could be any symbol taken from the basic character set, i.e., from the letters, the decimal digits, the underscore, and 21 special characters.
A character constant is a fixed valued character string.
The intrinsic data type character stores characters and strings. The length of the string can be specified by len specifier. If no length is specified, it is 1. You can refer individual characters within a string referring by position; the left most character is at position 1.
Character Declaration
Declaring a character type data is same as other variables −
type-specifier :: variable_name
For example,
character :: reply, sex
you can assign a value like,
reply = N sex = F
The following example demonstrates declaration and use of character data type −
program hello implicit none character(len = 15) :: surname, firstname character(len = 6) :: title character(len = 25)::greetings title = 'Mr. ' firstname = 'Rowan ' surname = 'Atkinson' greetings = 'A big hello from Mr. Bean' print *, 'Here is ', title, firstname, surname print *, greetings end program hello
When you compile and execute the above program it produces the following result −
Here is Mr. Rowan Atkinson A big hello from Mr. Bean
Concatenation of Characters
The concatenation operator //, concatenates characters.
The following example demonstrates this −
program hello implicit none character(len = 15) :: surname, firstname character(len = 6) :: title character(len = 40):: name character(len = 25)::greetings title = 'Mr. ' firstname = 'Rowan ' surname = 'Atkinson' name = title//firstname//surname greetings = 'A big hello from Mr. Bean' print *, 'Here is ', name print *, greetings end program hello
When you compile and execute the above program it produces the following result −
Here is Mr.Rowan Atkinson A big hello from Mr.Bean
Some Character Functions
The following table shows some commonly used character functions along with the description −
| Sr.No | Function & Description |
|---|---|
| 1 |
len(string) It returns the length of a character string |
| 2 |
index(string,sustring) It nds the location of a substring in another string, returns 0 if not found. |
| 3 |
achar(int) It converts an integer into a character |
| 4 |
iachar(c) It converts a character into an integer |
| 5 |
trim(string) It returns the string with the trailing blanks removed. |
| 6 |
scan(string, chars) It searches the "string" from left to right (unless back=.true.) for the first occurrence of any character contained in "chars". It returns an integer giving the position of that character, or zero if none of the characters in "chars" have been found. |
| 7 |
verify(string, chars) It scans the "string" from left to right (unless back=.true.) for the first occurrence of any character not contained in "chars". It returns an integer giving the position of that character, or zero if only the characters in "chars" have been found |
| 8 |
adjustl(string) It left justifies characters contained in the "string" |
| 9 |
adjustr(string) It right justifies characters contained in the "string" |
| 10 |
len_trim(string) It returns an integer equal to the length of "string" (len(string)) minus the number of trailing blanks |
| 11 |
repeat(string,ncopy) It returns a string with length equal to "ncopy" times the length of "string", and containing "ncopy" concatenated copies of "string" |
Example 1
This example shows the use of the index function −
program testingChars
implicit none
character (80) :: text
integer :: i
text = 'The intrinsic data type character stores characters and strings.'
i=index(text,'character')
if (i /= 0) then
print *, ' The word character found at position ',i
print *, ' in text: ', text
end if
end program testingChars
When you compile and execute the above program it produces the following result −
The word character found at position 25 in text : The intrinsic data type character stores characters and strings.
Example 2
This example demonstrates the use of the trim function −
program hello implicit none character(len = 15) :: surname, firstname character(len = 6) :: title character(len = 25)::greetings title = 'Mr.' firstname = 'Rowan' surname = 'Atkinson' print *, 'Here is', title, firstname, surname print *, 'Here is', trim(title),' ',trim(firstname),' ', trim(surname) end program hello
When you compile and execute the above program it produces the following result −
Here isMr. Rowan Atkinson Here isMr. Rowan Atkinson
Example 3
This example demonstrates the use of achar function −
program testingChars
implicit none
character:: ch
integer:: i
do i = 65, 90
ch = achar(i)
print*, i, ' ', ch
end do
end program testingChars
When you compile and execute the above program it produces the following result −
65 A 66 B 67 C 68 D 69 E 70 F 71 G 72 H 73 I 74 J 75 K 76 L 77 M 78 N 79 O 80 P 81 Q 82 R 83 S 84 T 85 U 86 V 87 W 88 X 89 Y 90 Z
Checking Lexical Order of Characters
The following functions determine the lexical sequence of characters −
| Sr.No | Function & Description |
|---|---|
| 1 |
lle(char, char) Compares whether the first character is lexically less than or equal to the second |
| 2 |
lge(char, char) Compares whether the first character is lexically greater than or equal to the second |
| 3 |
lgt(char, char) Compares whether the first character is lexically greater than the second |
| 4 |
llt(char, char) Compares whether the first character is lexically less than the second |
Example 4
The following function demonstrates the use −
program testingChars
implicit none
character:: a, b, c
a = 'A'
b = 'a'
c = 'B'
if(lgt(a,b)) then
print *, 'A is lexically greater than a'
else
print *, 'a is lexically greater than A'
end if
if(lgt(a,c)) then
print *, 'A is lexically greater than B'
else
print *, 'B is lexically greater than A'
end if
if(llt(a,b)) then
print *, 'A is lexically less than a'
end if
if(llt(a,c)) then
print *, 'A is lexically less than B'
end if
end program testingChars
When you compile and execute the above program it produces the following result −
a is lexically greater than A B is lexically greater than A A is lexically less than a A is lexically less than B
Fortran - Strings
The Fortran language can treat characters as single character or contiguous strings.
A character string may be only one character in length, or it could even be of zero length. In Fortran, character constants are given between a pair of double or single quotes.
The intrinsic data type character stores characters and strings. The length of the string can be specified by len specifier. If no length is specified, it is 1. You can refer individual characters within a string referring by position; the left most character is at position 1.
String Declaration
Declaring a string is same as other variables −
type-specifier :: variable_name
For example,
Character(len = 20) :: firstname, surname
you can assign a value like,
character (len = 40) :: name name = Zara Ali
The following example demonstrates declaration and use of character data type −
program hello implicit none character(len = 15) :: surname, firstname character(len = 6) :: title character(len = 25)::greetings title = 'Mr.' firstname = 'Rowan' surname = 'Atkinson' greetings = 'A big hello from Mr. Beans' print *, 'Here is', title, firstname, surname print *, greetings end program hello
When you compile and execute the above program it produces the following result −
Here isMr. Rowan Atkinson A big hello from Mr. Bean
String Concatenation
The concatenation operator //, concatenates strings.
The following example demonstrates this −
program hello implicit none character(len = 15) :: surname, firstname character(len = 6) :: title character(len = 40):: name character(len = 25)::greetings title = 'Mr.' firstname = 'Rowan' surname = 'Atkinson' name = title//firstname//surname greetings = 'A big hello from Mr. Beans' print *, 'Here is', name print *, greetings end program hello
When you compile and execute the above program it produces the following result −
Here is Mr. Rowan Atkinson A big hello from Mr. Bean
Extracting Substrings
In Fortran, you can extract a substring from a string by indexing the string, giving the start and the end index of the substring in a pair of brackets. This is called extent specifier.
The following example shows how to extract the substring world from the string hello world −
program subString character(len = 11)::hello hello = "Hello World" print*, hello(7:11) end program subString
When you compile and execute the above program it produces the following result −
World
Example
The following example uses the date_and_time function to give the date and time string. We use extent specifiers to extract the year, date, month, hour, minutes and second information separately.
program datetime implicit none character(len = 8) :: dateinfo ! ccyymmdd character(len = 4) :: year, month*2, day*2 character(len = 10) :: timeinfo ! hhmmss.sss character(len = 2) :: hour, minute, second*6 call date_and_time(dateinfo, timeinfo) ! lets break dateinfo into year, month and day. ! dateinfo has a form of ccyymmdd, where cc = century, yy = year ! mm = month and dd = day year = dateinfo(1:4) month = dateinfo(5:6) day = dateinfo(7:8) print*, 'Date String:', dateinfo print*, 'Year:', year print *,'Month:', month print *,'Day:', day ! lets break timeinfo into hour, minute and second. ! timeinfo has a form of hhmmss.sss, where h = hour, m = minute ! and s = second hour = timeinfo(1:2) minute = timeinfo(3:4) second = timeinfo(5:10) print*, 'Time String:', timeinfo print*, 'Hour:', hour print*, 'Minute:', minute print*, 'Second:', second end program datetime
When you compile and execute the above program, it gives the detailed date and time information −
Date String: 20140803 Year: 2014 Month: 08 Day: 03 Time String: 075835.466 Hour: 07 Minute: 58 Second: 35.466
Trimming Strings
The trim function takes a string, and returns the input string after removing all trailing blanks.
Example
program trimString implicit none character (len = *), parameter :: fname="Susanne", sname="Rizwan" character (len = 20) :: fullname fullname = fname//" "//sname !concatenating the strings print*,fullname,", the beautiful dancer from the east!" print*,trim(fullname),", the beautiful dancer from the east!" end program trimString
When you compile and execute the above program it produces the following result −
Susanne Rizwan , the beautiful dancer from the east! Susanne Rizwan, the beautiful dancer from the east!
Left and Right Adjustment of Strings
The function adjustl takes a string and returns it by removing the leading blanks and appending them as trailing blanks.
The function adjustr takes a string and returns it by removing the trailing blanks and appending them as leading blanks.
Example
program hello implicit none character(len = 15) :: surname, firstname character(len = 6) :: title character(len = 40):: name character(len = 25):: greetings title = 'Mr. ' firstname = 'Rowan' surname = 'Atkinson' greetings = 'A big hello from Mr. Beans' name = adjustl(title)//adjustl(firstname)//adjustl(surname) print *, 'Here is', name print *, greetings name = adjustr(title)//adjustr(firstname)//adjustr(surname) print *, 'Here is', name print *, greetings name = trim(title)//trim(firstname)//trim(surname) print *, 'Here is', name print *, greetings end program hello
When you compile and execute the above program it produces the following result −
Here is Mr. Rowan Atkinson A big hello from Mr. Bean Here is Mr. Rowan Atkinson A big hello from Mr. Bean Here is Mr.RowanAtkinson A big hello from Mr. Bean
Searching for a Substring in a String
The index function takes two strings and checks if the second string is a substring of the first string. If the second argument is a substring of the first argument, then it returns an integer which is the starting index of the second string in the first string, else it returns zero.
Example
program hello
implicit none
character(len=30) :: myString
character(len=10) :: testString
myString = 'This is a test'
testString = 'test'
if(index(myString, testString) == 0)then
print *, 'test is not found'
else
print *, 'test is found at index: ', index(myString, testString)
end if
end program hello
When you compile and execute the above program it produces the following result −
test is found at index: 11
Fortran - Arrays
Arrays can store a fixed-size sequential collection of elements of the same type. An array is used to store a collection of data, but it is often more useful to think of an array as a collection of variables of the same type.
All arrays consist of contiguous memory locations. The lowest address corresponds to the first element and the highest address to the last element.
| Numbers(1) | Numbers(2) | Numbers(3) | Numbers(4) |
Arrays can be one- dimensional (like vectors), two-dimensional (like matrices) and Fortran allows you to create up to 7-dimensional arrays.
Declaring Arrays
Arrays are declared with the dimension attribute.
For example, to declare a one-dimensional array named number, of real numbers containing 5 elements, you write,
real, dimension(5) :: numbers
The individual elements of arrays are referenced by specifying their subscripts. The first element of an array has a subscript of one. The array numbers contains five real variables numbers(1), numbers(2), numbers(3), numbers(4), and numbers(5).
To create a 5 x 5 two-dimensional array of integers named matrix, you write −
integer, dimension (5,5) :: matrix
You can also declare an array with some explicit lower bound, for example −
real, dimension(2:6) :: numbers integer, dimension (-3:2,0:4) :: matrix
Assigning Values
You can either assign values to individual members, like,
numbers(1) = 2.0
or, you can use a loop,
do i =1,5 numbers(i) = i * 2.0 end do
One-dimensional array elements can be directly assigned values using a short hand symbol, called array constructor, like,
numbers = (/1.5, 3.2,4.5,0.9,7.2 /)
please note that there are no spaces allowed between the brackets ( and the back slash /
Example
The following example demonstrates the concepts discussed above.
program arrayProg
real :: numbers(5) !one dimensional integer array
integer :: matrix(3,3), i , j !two dimensional real array
!assigning some values to the array numbers
do i=1,5
numbers(i) = i * 2.0
end do
!display the values
do i = 1, 5
Print *, numbers(i)
end do
!assigning some values to the array matrix
do i=1,3
do j = 1, 3
matrix(i, j) = i+j
end do
end do
!display the values
do i=1,3
do j = 1, 3
Print *, matrix(i,j)
end do
end do
!short hand assignment
numbers = (/1.5, 3.2,4.5,0.9,7.2 /)
!display the values
do i = 1, 5
Print *, numbers(i)
end do
end program arrayProg
When the above code is compiled and executed, it produces the following result −
2.00000000
4.00000000
6.00000000
8.00000000
10.0000000
2
3
4
3
4
5
4
5
6
1.50000000
3.20000005
4.50000000
0.899999976
7.19999981
Some Array Related Terms
The following table gives some array related terms −
| Term | Meaning |
|---|---|
| Rank | It is the number of dimensions an array has. For example, for the array named matrix, rank is 2, and for the array named numbers, rank is 1. |
| Extent | It is the number of elements along a dimension. For example, the array numbers has extent 5 and the array named matrix has extent 3 in both dimensions. |
| Shape | The shape of an array is a one-dimensional integer array, containing the number of elements (the extent) in each dimension. For example, for the array matrix, shape is (3, 3) and the array numbers it is (5). |
| Size | It is the number of elements an array contains. For the array matrix, it is 9, and for the array numbers, it is 5. |
Passing Arrays to Procedures
You can pass an array to a procedure as an argument. The following example demonstrates the concept −
program arrayToProcedure
implicit none
integer, dimension (5) :: myArray
integer :: i
call fillArray (myArray)
call printArray(myArray)
end program arrayToProcedure
subroutine fillArray (a)
implicit none
integer, dimension (5), intent (out) :: a
! local variables
integer :: i
do i = 1, 5
a(i) = i
end do
end subroutine fillArray
subroutine printArray(a)
integer, dimension (5) :: a
integer::i
do i = 1, 5
Print *, a(i)
end do
end subroutine printArray
When the above code is compiled and executed, it produces the following result −
1 2 3 4 5
In the above example, the subroutine fillArray and printArray can only be called with arrays with dimension 5. However, to write subroutines that can be used for arrays of any size, you can rewrite it using the following technique −
program arrayToProcedure
implicit none
integer, dimension (10) :: myArray
integer :: i
interface
subroutine fillArray (a)
integer, dimension(:), intent (out) :: a
integer :: i
end subroutine fillArray
subroutine printArray (a)
integer, dimension(:) :: a
integer :: i
end subroutine printArray
end interface
call fillArray (myArray)
call printArray(myArray)
end program arrayToProcedure
subroutine fillArray (a)
implicit none
integer,dimension (:), intent (out) :: a
! local variables
integer :: i, arraySize
arraySize = size(a)
do i = 1, arraySize
a(i) = i
end do
end subroutine fillArray
subroutine printArray(a)
implicit none
integer,dimension (:) :: a
integer::i, arraySize
arraySize = size(a)
do i = 1, arraySize
Print *, a(i)
end do
end subroutine printArray
Please note that the program is using the size function to get the size of the array.
When the above code is compiled and executed, it produces the following result −
1 2 3 4 5 6 7 8 9 10
Array Sections
So far we have referred to the whole array, Fortran provides an easy way to refer several elements, or a section of an array, using a single statement.
To access an array section, you need to provide the lower and the upper bound of the section, as well as a stride (increment), for all the dimensions. This notation is called a subscript triplet:
array ([lower]:[upper][:stride], ...)
When no lower and upper bounds are mentioned, it defaults to the extents you declared, and stride value defaults to 1.
The following example demonstrates the concept −
program arraySubsection
real, dimension(10) :: a, b
integer:: i, asize, bsize
a(1:7) = 5.0 ! a(1) to a(7) assigned 5.0
a(8:) = 0.0 ! rest are 0.0
b(2:10:2) = 3.9
b(1:9:2) = 2.5
!display
asize = size(a)
bsize = size(b)
do i = 1, asize
Print *, a(i)
end do
do i = 1, bsize
Print *, b(i)
end do
end program arraySubsection
When the above code is compiled and executed, it produces the following result −
5.00000000 5.00000000 5.00000000 5.00000000 5.00000000 5.00000000 5.00000000 0.00000000E+00 0.00000000E+00 0.00000000E+00 2.50000000 3.90000010 2.50000000 3.90000010 2.50000000 3.90000010 2.50000000 3.90000010 2.50000000 3.90000010
Array Intrinsic Functions
Fortran 90/95 provides several intrinsic procedures. They can be divided into 7 categories.
Fortran - Dynamic Arrays
A dynamic array is an array, the size of which is not known at compile time, but will be known at execution time.
Dynamic arrays are declared with the attribute allocatable.
For example,
real, dimension (:,:), allocatable :: darray
The rank of the array, i.e., the dimensions has to be mentioned however, to allocate memory to such an array, you use the allocate function.
allocate ( darray(s1,s2) )
After the array is used, in the program, the memory created should be freed using the deallocate function
deallocate (darray)
Example
The following example demonstrates the concepts discussed above.
program dynamic_array
implicit none
!rank is 2, but size not known
real, dimension (:,:), allocatable :: darray
integer :: s1, s2
integer :: i, j
print*, "Enter the size of the array:"
read*, s1, s2
! allocate memory
allocate ( darray(s1,s2) )
do i = 1, s1
do j = 1, s2
darray(i,j) = i*j
print*, "darray(",i,",",j,") = ", darray(i,j)
end do
end do
deallocate (darray)
end program dynamic_array
When the above code is compiled and executed, it produces the following result −
Enter the size of the array: 3,4 darray( 1 , 1 ) = 1.00000000 darray( 1 , 2 ) = 2.00000000 darray( 1 , 3 ) = 3.00000000 darray( 1 , 4 ) = 4.00000000 darray( 2 , 1 ) = 2.00000000 darray( 2 , 2 ) = 4.00000000 darray( 2 , 3 ) = 6.00000000 darray( 2 , 4 ) = 8.00000000 darray( 3 , 1 ) = 3.00000000 darray( 3 , 2 ) = 6.00000000 darray( 3 , 3 ) = 9.00000000 darray( 3 , 4 ) = 12.0000000
Use of Data Statement
The data statement can be used for initialising more than one array, or for array section initialisation.
The syntax of data statement is −
data variable / list / ...
Example
The following example demonstrates the concept −
program dataStatement
implicit none
integer :: a(5), b(3,3), c(10),i, j
data a /7,8,9,10,11/
data b(1,:) /1,1,1/
data b(2,:)/2,2,2/
data b(3,:)/3,3,3/
data (c(i),i = 1,10,2) /4,5,6,7,8/
data (c(i),i = 2,10,2)/5*2/
Print *, 'The A array:'
do j = 1, 5
print*, a(j)
end do
Print *, 'The B array:'
do i = lbound(b,1), ubound(b,1)
write(*,*) (b(i,j), j = lbound(b,2), ubound(b,2))
end do
Print *, 'The C array:'
do j = 1, 10
print*, c(j)
end do
end program dataStatement
When the above code is compiled and executed, it produces the following result −
The A array:
7
8
9
10
11
The B array:
1 1 1
2 2 2
3 3 3
The C array:
4
2
5
2
6
2
7
2
8
2
Use of Where Statement
The where statement allows you to use some elements of an array in an expression, depending on the outcome of some logical condition. It allows the execution of the expression, on an element, if the given condition is true.
Example
The following example demonstrates the concept −
program whereStatement
implicit none
integer :: a(3,5), i , j
do i = 1,3
do j = 1, 5
a(i,j) = j-i
end do
end do
Print *, 'The A array:'
do i = lbound(a,1), ubound(a,1)
write(*,*) (a(i,j), j = lbound(a,2), ubound(a,2))
end do
where( a<0 )
a = 1
elsewhere
a = 5
end where
Print *, 'The A array:'
do i = lbound(a,1), ubound(a,1)
write(*,*) (a(i,j), j = lbound(a,2), ubound(a,2))
end do
end program whereStatement
When the above code is compiled and executed, it produces the following result −
The A array:
0 1 2 3 4
-1 0 1 2 3
-2 -1 0 1 2
The A array:
5 5 5 5 5
1 5 5 5 5
1 1 5 5 5
Fortran - Derived Data Types
Fortran allows you to define derived data types. A derived data type is also called a structure, and it can consist of data objects of different types.
Derived data types are used to represent a record. E.g. you want to keep track of your books in a library, you might want to track the following attributes about each book −
- Title
- Author
- Subject
- Book ID
Defining a Derived data type
To define a derived data type, the type and end type statements are used. . The type statement defines a new data type, with more than one member for your program. The format of the type statement is this −
type type_name declarations end type
Here is the way you would declare the Book structure −
type Books character(len = 50) :: title character(len = 50) :: author character(len = 150) :: subject integer :: book_id end type Books
Accessing Structure Members
An object of a derived data type is called a structure.
A structure of type Books can be created in a type declaration statement like −
type(Books) :: book1
The components of the structure can be accessed using the component selector character (%) −
book1%title = "C Programming" book1%author = "Nuha Ali" book1%subject = "C Programming Tutorial" book1%book_id = 6495407
Note that there are no spaces before and after the % symbol.
Example
The following program illustrates the above concepts −
program deriveDataType
!type declaration
type Books
character(len = 50) :: title
character(len = 50) :: author
character(len = 150) :: subject
integer :: book_id
end type Books
!declaring type variables
type(Books) :: book1
type(Books) :: book2
!accessing the components of the structure
book1%title = "C Programming"
book1%author = "Nuha Ali"
book1%subject = "C Programming Tutorial"
book1%book_id = 6495407
book2%title = "Telecom Billing"
book2%author = "Zara Ali"
book2%subject = "Telecom Billing Tutorial"
book2%book_id = 6495700
!display book info
Print *, book1%title
Print *, book1%author
Print *, book1%subject
Print *, book1%book_id
Print *, book2%title
Print *, book2%author
Print *, book2%subject
Print *, book2%book_id
end program deriveDataType
When the above code is compiled and executed, it produces the following result −
C Programming Nuha Ali C Programming Tutorial 6495407 Telecom Billing Zara Ali Telecom Billing Tutorial 6495700
Array of Structures
You can also create arrays of a derived type −
type(Books), dimension(2) :: list
Individual elements of the array could be accessed as −
list(1)%title = "C Programming" list(1)%author = "Nuha Ali" list(1)%subject = "C Programming Tutorial" list(1)%book_id = 6495407
The following program illustrates the concept −
program deriveDataType
!type declaration
type Books
character(len = 50) :: title
character(len = 50) :: author
character(len = 150) :: subject
integer :: book_id
end type Books
!declaring array of books
type(Books), dimension(2) :: list
!accessing the components of the structure
list(1)%title = "C Programming"
list(1)%author = "Nuha Ali"
list(1)%subject = "C Programming Tutorial"
list(1)%book_id = 6495407
list(2)%title = "Telecom Billing"
list(2)%author = "Zara Ali"
list(2)%subject = "Telecom Billing Tutorial"
list(2)%book_id = 6495700
!display book info
Print *, list(1)%title
Print *, list(1)%author
Print *, list(1)%subject
Print *, list(1)%book_id
Print *, list(1)%title
Print *, list(2)%author
Print *, list(2)%subject
Print *, list(2)%book_id
end program deriveDataType
When the above code is compiled and executed, it produces the following result −
C Programming Nuha Ali C Programming Tutorial 6495407 C Programming Zara Ali Telecom Billing Tutorial 6495700
Fortran - Pointers
In most programming languages, a pointer variable stores the memory address of an object. However, in Fortran, a pointer is a data object that has more functionalities than just storing the memory address. It contains more information about a particular object, like type, rank, extents, and memory address.
A pointer is associated with a target by allocation or pointer assignment.
Declaring a Pointer Variable
A pointer variable is declared with the pointer attribute.
The following examples shows declaration of pointer variables −
integer, pointer :: p1 ! pointer to integer real, pointer, dimension (:) :: pra ! pointer to 1-dim real array real, pointer, dimension (:,:) :: pra2 ! pointer to 2-dim real array
A pointer can point to −
An area of dynamically allocated memory.
A data object of the same type as the pointer, with the target attribute.
Allocating Space for a Pointer
The allocate statement allows you to allocate space for a pointer object. For example −
program pointerExample implicit none integer, pointer :: p1 allocate(p1) p1 = 1 Print *, p1 p1 = p1 + 4 Print *, p1 end program pointerExample
When the above code is compiled and executed, it produces the following result −
1 5
You should empty the allocated storage space by the deallocate statement when it is no longer required and avoid accumulation of unused and unusable memory space.
Targets and Association
A target is another normal variable, with space set aside for it. A target variable must be declared with the target attribute.
You associate a pointer variable with a target variable using the association operator (=>).
Let us rewrite the previous example, to demonstrate the concept −
program pointerExample implicit none integer, pointer :: p1 integer, target :: t1 p1=>t1 p1 = 1 Print *, p1 Print *, t1 p1 = p1 + 4 Print *, p1 Print *, t1 t1 = 8 Print *, p1 Print *, t1 end program pointerExample
When the above code is compiled and executed, it produces the following result −
1 1 5 5 8 8
A pointer can be −
- Undefined
- Associated
- Disassociated
In the above program, we have associated the pointer p1, with the target t1, using the => operator. The function associated, tests a pointers association status.
The nullify statement disassociates a pointer from a target.
Nullify does not empty the targets as there could be more than one pointer pointing to the same target. However, emptying the pointer implies nullification also.
Example 1
The following example demonstrates the concepts −
program pointerExample implicit none integer, pointer :: p1 integer, target :: t1 integer, target :: t2 p1=>t1 p1 = 1 Print *, p1 Print *, t1 p1 = p1 + 4 Print *, p1 Print *, t1 t1 = 8 Print *, p1 Print *, t1 nullify(p1) Print *, t1 p1=>t2 Print *, associated(p1) Print*, associated(p1, t1) Print*, associated(p1, t2) !what is the value of p1 at present Print *, p1 Print *, t2 p1 = 10 Print *, p1 Print *, t2 end program pointerExample
When the above code is compiled and executed, it produces the following result −
1 1 5 5 8 8 8 T F T 952754640 952754640 10 10
Please note that each time you run the code, the memory addresses will be different.
Example 2
program pointerExample implicit none integer, pointer :: a, b integer, target :: t integer :: n t = 1 a => t t = 2 b => t n = a + b Print *, a, b, t, n end program pointerExample
When the above code is compiled and executed, it produces the following result −
2 2 2 4
Fortran - Basic Input Output
We have so far seen that we can read data from keyboard using the read * statement, and display output to the screen using the print* statement, respectively. This form of input-output is free format I/O, and it is called list-directed input-output.
The free format simple I/O has the form −
read(*,*) item1, item2, item3... print *, item1, item2, item3 write(*,*) item1, item2, item3...
However the formatted I/O gives you more flexibility over data transfer.
Formatted Input Output
Formatted input output has the syntax as follows −
read fmt, variable_list print fmt, variable_list write fmt, variable_list
Where,
fmt is the format specification
variable-list is a list of the variables to be read from keyboard or written on screen
Format specification defines the way in which formatted data is displayed. It consists of a string, containing a list of edit descriptors in parentheses.
An edit descriptor specifies the exact format, for example, width, digits after decimal point etc., in which characters and numbers are displayed.
For example
Print "(f6.3)", pi
The following table describes the descriptors −
| Descriptor | Description | Example |
|---|---|---|
| I | This is used for integer output. This takes the form rIw.m where the meanings of r, w and m are given in the table below. Integer values are right justied in their elds. If the eld width is not large enough to accommodate an integer then the eld is lled with asterisks. |
print "(3i5)", i, j, k |
| F | This is used for real number output. This takes the form rFw.d where the meanings of r, w and d are given in the table below. Real values are right justied in their elds. If the eld width is not large enough to accommodate the real number then the eld is lled with asterisks. |
print "(f12.3)",pi |
| E |
This is used for real output in exponential notation. The E descriptor statement takes the form rEw.d where the meanings of r, w and d are given in the table below. Real values are right justied in their elds. If the eld width is not large enough to accommodate the real number then the eld is lled with asterisks. Please note that, to print out a real number with three decimal places a eld width of at least ten is needed. One for the sign of the mantissa, two for the zero, four for the mantissa and two for the exponent itself. In general, w ≥ d + 7. |
print "(e10.3)",123456.0 gives 0.123e+06 |
| ES | This is used for real output (scientific notation). This takes the form rESw.d where the meanings of r, w and d are given in the table below. The E descriptor described above diers slightly from the traditional well known scientic notation. Scientic notation has the mantissa in the range 1.0 to 10.0 unlike the E descriptor which has the mantissa in the range 0.1 to 1.0. Real values are right justied in their elds. If the eld width is not large enough to accommodate the real number then the eld is lled with asterisks. Here also, the width eld must satisfy the expressionw ≥ d + 7 |
print "(es10.3)",123456.0 gives 1.235e+05 |
| A | This is used for character output. This takes the form rAw where the meanings of r and w are given in the table below. Character types are right justied in their elds. If the eld width is not large enough to accommodate the character string then the eld is lled with the rst w characters of the string. |
print "(a10)", str |
| X | This is used for space output. This takes the form nX where n is the number of desired spaces. |
print "(5x, a10)", str |
| / | Slash descriptor used to insert blank lines. This takes the form / and forces the next data output to be on a new line. |
print "(/,5x, a10)", str |
Following symbols are used with the format descriptors −
| Sr.No | Symbol & Description |
|---|---|
| 1 |
c Column number |
| 2 |
d Number of digits to right of the decimal place for real input or output |
| 3 |
m Minimum number of digits to be displayed |
| 4 |
n Number of spaces to skip |
| 5 |
r Repeat count the number of times to use a descriptor or group of descriptors |
| 6 |
w Field width the number of characters to use for the input or output |
Example 1
program printPi pi = 3.141592653589793238 Print "(f6.3)", pi Print "(f10.7)", pi Print "(f20.15)", pi Print "(e16.4)", pi/100 end program printPi
When the above code is compiled and executed, it produces the following result −
3.142 3.1415927 3.141592741012573 0.3142E-01
Example 2
program printName implicit none character (len = 15) :: first_name print *,' Enter your first name.' print *,' Up to 20 characters, please' read *,first_name print "(1x,a)",first_name end program printName
When the above code is compiled and executed, it produces the following result: (assume the user enters the name Zara)
Enter your first name. Up to 20 characters, please Zara
Example 3
program formattedPrint implicit none real :: c = 1.2786456e-9, d = 0.1234567e3 integer :: n = 300789, k = 45, i = 2 character (len=15) :: str="Tutorials Point" print "(i6)", k print "(i6.3)", k print "(3i10)", n, k, i print "(i10,i3,i5)", n, k, i print "(a15)",str print "(f12.3)", d print "(e12.4)", c print '(/,3x,"n = ",i6, 3x, "d = ",f7.4)', n, d end program formattedPrint
When the above code is compiled and executed, it produces the following result −
45 045 300789 45 2 300789 45 2 Tutorials Point 123.457 0.1279E-08 n = 300789 d = *******
The Format Statement
The format statement allows you to mix and match character, integer and real output in one statement. The following example demonstrates this −
program productDetails implicit none character (len = 15) :: name integer :: id real :: weight name = 'Ardupilot' id = 1 weight = 0.08 print *,' The product details are' print 100 100 format (7x,'Name:', 7x, 'Id:', 1x, 'Weight:') print 200, name, id, weight 200 format(1x, a, 2x, i3, 2x, f5.2) end program productDetails
When the above code is compiled and executed, it produces the following result −
The product details are Name: Id: Weight: Ardupilot 1 0.08
Fortran - File Input Output
Fortran allows you to read data from, and write data into files.
In the last chapter, you have seen how to read data from, and write data to the terminal. In this chapter you will study file input and output functionalities provided by Fortran.
You can read and write to one or more files. The OPEN, WRITE, READ and CLOSE statements allow you to achieve this.
Opening and Closing Files
Before using a file you must open the file. The open command is used to open files for reading or writing. The simplest form of the command is −
open (unit = number, file = "name").
However, the open statement may have a general form −
open (list-of-specifiers)
The following table describes the most commonly used specifiers −
| Sr.No | Specifier & Description |
|---|---|
| 1 |
[UNIT=] u The unit numberucould be any number in the range 9-99 and it indicates the file, you may choose any number but every open file in the program must have a unique number |
| 2 |
IOSTAT= ios It is the I/O status identifier and should be an integer variable. If the open statement is successful then the ios value returned is zero else a non-zero value. |
| 3 |
ERR = err It is a label to which the control jumps in case of any error. |
| 4 |
FILE = fname File name, a character string. |
| 5 |
STATUS = sta It shows the prior status of the file. A character string and can have one of the three values NEW, OLD or SCRATCH. A scratch file is created and deleted when closed or the program ends. |
| 6 |
ACCESS = acc It is the file access mode. Can have either of the two values, SEQUENTIAL or DIRECT. The default is SEQUENTIAL. |
| 7 |
FORM = frm It gives the formatting status of the file. Can have either of the two values FORMATTED or UNFORMATTED. The default is UNFORMATTED |
| 8 |
RECL = rl It specifies the length of each record in a direct access file. |
After the file has been opened, it is accessed by read and write statements. Once done, it should be closed using the close statement.
The close statement has the following syntax −
close ([UNIT = ]u[,IOSTAT = ios,ERR = err,STATUS = sta])
Please note that the parameters in brackets are optional.
Example
This example demonstrates opening a new file for writing some data into the file.
program outputdata
implicit none
real, dimension(100) :: x, y
real, dimension(100) :: p, q
integer :: i
! data
do i=1,100
x(i) = i * 0.1
y(i) = sin(x(i)) * (1-cos(x(i)/3.0))
end do
! output data into a file
open(1, file = 'data1.dat', status = 'new')
do i=1,100
write(1,*) x(i), y(i)
end do
close(1)
end program outputdata
When the above code is compiled and executed, it creates the file data1.dat and writes the x and y array values into it. And then closes the file.
Reading from and Writing into the File
The read and write statements respectively are used for reading from and writing into a file respectively.
They have the following syntax −
read ([UNIT = ]u, [FMT = ]fmt, IOSTAT = ios, ERR = err, END = s) write([UNIT = ]u, [FMT = ]fmt, IOSTAT = ios, ERR = err, END = s)
Most of the specifiers have already been discussed in the above table.
The END = s specifier is a statement label where the program jumps, when it reaches end-of-file.
Example
This example demonstrates reading from and writing into a file.
In this program we read from the file, we created in the last example, data1.dat, and display it on screen.
program outputdata
implicit none
real, dimension(100) :: x, y
real, dimension(100) :: p, q
integer :: i
! data
do i = 1,100
x(i) = i * 0.1
y(i) = sin(x(i)) * (1-cos(x(i)/3.0))
end do
! output data into a file
open(1, file = 'data1.dat', status='new')
do i = 1,100
write(1,*) x(i), y(i)
end do
close(1)
! opening the file for reading
open (2, file = 'data1.dat', status = 'old')
do i = 1,100
read(2,*) p(i), q(i)
end do
close(2)
do i = 1,100
write(*,*) p(i), q(i)
end do
end program outputdata
When the above code is compiled and executed, it produces the following result −
0.100000001 5.54589933E-05 0.200000003 4.41325130E-04 0.300000012 1.47636665E-03 0.400000006 3.45637114E-03 0.500000000 6.64328877E-03 0.600000024 1.12552457E-02 0.699999988 1.74576249E-02 0.800000012 2.53552198E-02 0.900000036 3.49861123E-02 1.00000000 4.63171229E-02 1.10000002 5.92407547E-02 1.20000005 7.35742599E-02 1.30000007 8.90605897E-02 1.39999998 0.105371222 1.50000000 0.122110792 1.60000002 0.138823599 1.70000005 0.155002072 1.80000007 0.170096487 1.89999998 0.183526158 2.00000000 0.194692180 2.10000014 0.202990443 2.20000005 0.207826138 2.29999995 0.208628103 2.40000010 0.204863414 2.50000000 0.196052119 2.60000014 0.181780845 2.70000005 0.161716297 2.79999995 0.135617107 2.90000010 0.103344671 3.00000000 6.48725405E-02 3.10000014 2.02930309E-02 3.20000005 -3.01767997E-02 3.29999995 -8.61928314E-02 3.40000010 -0.147283033 3.50000000 -0.212848678 3.60000014 -0.282169819 3.70000005 -0.354410470 3.79999995 -0.428629100 3.90000010 -0.503789663 4.00000000 -0.578774154 4.09999990 -0.652400017 4.20000029 -0.723436713 4.30000019 -0.790623367 4.40000010 -0.852691114 4.50000000 -0.908382416 4.59999990 -0.956472993 4.70000029 -0.995793998 4.80000019 -1.02525222 4.90000010 -1.04385209 5.00000000 -1.05071592 5.09999990 -1.04510069 5.20000029 -1.02641726 5.30000019 -0.994243503 5.40000010 -0.948338211 5.50000000 -0.888650239 5.59999990 -0.815326691 5.70000029 -0.728716135 5.80000019 -0.629372001 5.90000010 -0.518047631 6.00000000 -0.395693362 6.09999990 -0.263447165 6.20000029 -0.122622721 6.30000019 2.53026206E-02 6.40000010 0.178709000 6.50000000 0.335851669 6.59999990 0.494883657 6.70000029 0.653881252 6.80000019 0.810866773 6.90000010 0.963840425 7.00000000 1.11080539 7.09999990 1.24979746 7.20000029 1.37891412 7.30000019 1.49633956 7.40000010 1.60037732 7.50000000 1.68947268 7.59999990 1.76223695 7.70000029 1.81747139 7.80000019 1.85418403 7.90000010 1.87160957 8.00000000 1.86922085 8.10000038 1.84674001 8.19999981 1.80414569 8.30000019 1.74167395 8.40000057 1.65982044 8.50000000 1.55933595 8.60000038 1.44121361 8.69999981 1.30668485 8.80000019 1.15719533 8.90000057 0.994394958 9.00000000 0.820112705 9.10000038 0.636327863 9.19999981 0.445154816 9.30000019 0.248800844 9.40000057 4.95488606E-02 9.50000000 -0.150278628 9.60000038 -0.348357052 9.69999981 -0.542378068 9.80000019 -0.730095863 9.90000057 -0.909344316 10.0000000 -1.07807255
Fortran - Procedures
A procedure is a group of statements that perform a well-defined task and can be invoked from your program. Information (or data) is passed to the calling program, to the procedure as arguments.
There are two types of procedures −
- Functions
- Subroutines
Function
A function is a procedure that returns a single quantity. A function should not modify its arguments.
The returned quantity is known as function value, and it is denoted by the function name.
Syntax
Syntax for a function is as follows −
function name(arg1, arg2, ....) [declarations, including those for the arguments] [executable statements] end function [name]
The following example demonstrates a function named area_of_circle. It calculates the area of a circle with radius r.
program calling_func real :: a a = area_of_circle(2.0) Print *, "The area of a circle with radius 2.0 is" Print *, a end program calling_func ! this function computes the area of a circle with radius r function area_of_circle (r) ! function result implicit none ! dummy arguments real :: area_of_circle ! local variables real :: r real :: pi pi = 4 * atan (1.0) area_of_circle = pi * r**2 end function area_of_circle
When you compile and execute the above program, it produces the following result −
The area of a circle with radius 2.0 is 12.5663710
Please note that −
You must specify implicit none in both the main program as well as the procedure.
The argument r in the called function is called dummy argument.
The result Option
If you want the returned value to be stored in some other name than the function name, you can use the result option.
You can specify the return variable name as −
function name(arg1, arg2, ....) result (return_var_name) [declarations, including those for the arguments] [executable statements] end function [name]
Subroutine
A subroutine does not return a value, however it can modify its arguments.
Syntax
subroutine name(arg1, arg2, ....) [declarations, including those for the arguments] [executable statements] end subroutine [name]
Calling a Subroutine
You need to invoke a subroutine using the call statement.
The following example demonstrates the definition and use of a subroutine swap, that changes the values of its arguments.
program calling_func implicit none real :: a, b a = 2.0 b = 3.0 Print *, "Before calling swap" Print *, "a = ", a Print *, "b = ", b call swap(a, b) Print *, "After calling swap" Print *, "a = ", a Print *, "b = ", b end program calling_func subroutine swap(x, y) implicit none real :: x, y, temp temp = x x = y y = temp end subroutine swap
When you compile and execute the above program, it produces the following result −
Before calling swap a = 2.00000000 b = 3.00000000 After calling swap a = 3.00000000 b = 2.00000000
Specifying the Intent of the Arguments
The intent attribute allows you to specify the intention with which arguments are used in the procedure. The following table provides the values of the intent attribute −
| Value | Used as | Explanation |
|---|---|---|
| in | intent(in) | Used as input values, not changed in the function |
| out | intent(out) | Used as output value, they are overwritten |
| inout | intent(inout) | Arguments are both used and overwritten |
The following example demonstrates the concept −
program calling_func implicit none real :: x, y, z, disc x = 1.0 y = 5.0 z = 2.0 call intent_example(x, y, z, disc) Print *, "The value of the discriminant is" Print *, disc end program calling_func subroutine intent_example (a, b, c, d) implicit none ! dummy arguments real, intent (in) :: a real, intent (in) :: b real, intent (in) :: c real, intent (out) :: d d = b * b - 4.0 * a * c end subroutine intent_example
When you compile and execute the above program, it produces the following result −
The value of the discriminant is 17.0000000
Recursive Procedures
Recursion occurs when a programming languages allows you to call a function inside the same function. It is called recursive call of the function.
When a procedure calls itself, directly or indirectly, is called a recursive procedure. You should declare this type of procedures by preceding the word recursive before its declaration.
When a function is used recursively, the result option has to be used.
Following is an example, which calculates factorial for a given number using a recursive procedure −
program calling_func
implicit none
integer :: i, f
i = 15
Print *, "The value of factorial 15 is"
f = myfactorial(15)
Print *, f
end program calling_func
! computes the factorial of n (n!)
recursive function myfactorial (n) result (fac)
! function result
implicit none
! dummy arguments
integer :: fac
integer, intent (in) :: n
select case (n)
case (0:1)
fac = 1
case default
fac = n * myfactorial (n-1)
end select
end function myfactorial
Internal Procedures
When a procedure is contained within a program, it is called the internal procedure of the program. The syntax for containing an internal procedure is as follows −
program program_name implicit none ! type declaration statements ! executable statements . . . contains ! internal procedures . . . end program program_name
The following example demonstrates the concept −
program mainprog
implicit none
real :: a, b
a = 2.0
b = 3.0
Print *, "Before calling swap"
Print *, "a = ", a
Print *, "b = ", b
call swap(a, b)
Print *, "After calling swap"
Print *, "a = ", a
Print *, "b = ", b
contains
subroutine swap(x, y)
real :: x, y, temp
temp = x
x = y
y = temp
end subroutine swap
end program mainprog
When you compile and execute the above program, it produces the following result −
Before calling swap a = 2.00000000 b = 3.00000000 After calling swap a = 3.00000000 b = 2.00000000
Fortran - Modules
A module is like a package where you can keep your functions and subroutines, in case you are writing a very big program, or your functions or subroutines can be used in more than one program.
Modules provide you a way of splitting your programs between multiple files.
Modules are used for −
Packaging subprograms, data and interface blocks.
Defining global data that can be used by more than one routine.
Declaring variables that can be made available within any routines you choose.
Importing a module entirely, for use, into another program or subroutine.
Syntax of a Module
A module consists of two parts −
- a specification part for statements declaration
- a contains part for subroutine and function definitions
The general form of a module is −
module name [statement declarations] [contains [subroutine and function definitions] ] end module [name]
Using a Module into your Program
You can incorporate a module in a program or subroutine by the use statement −
use name
Please note that
You can add as many modules as needed, each will be in separate files and compiled separately.
A module can be used in various different programs.
A module can be used many times in the same program.
The variables declared in a module specification part, are global to the module.
The variables declared in a module become global variables in any program or routine where the module is used.
The use statement can appear in the main program, or any other subroutine or module which uses the routines or variables declared in a particular module.
Example
The following example demonstrates the concept −
module constants
implicit none
real, parameter :: pi = 3.1415926536
real, parameter :: e = 2.7182818285
contains
subroutine show_consts()
print*, "Pi = ", pi
print*, "e = ", e
end subroutine show_consts
end module constants
program module_example
use constants
implicit none
real :: x, ePowerx, area, radius
x = 2.0
radius = 7.0
ePowerx = e ** x
area = pi * radius**2
call show_consts()
print*, "e raised to the power of 2.0 = ", ePowerx
print*, "Area of a circle with radius 7.0 = ", area
end program module_example
When you compile and execute the above program, it produces the following result −
Pi = 3.14159274 e = 2.71828175 e raised to the power of 2.0 = 7.38905573 Area of a circle with radius 7.0 = 153.938049
Accessibility of Variables and Subroutines in a Module
By default, all the variables and subroutines in a module is made available to the program that is using the module code, by the use statement.
However, you can control the accessibility of module code using the private and public attributes. When you declare some variable or subroutine as private, it is not available outside the module.
Example
The following example illustrates the concept −
In the previous example, we had two module variables, e and pi. Let us make them private and observe the output −
module constants
implicit none
real, parameter,private :: pi = 3.1415926536
real, parameter, private :: e = 2.7182818285
contains
subroutine show_consts()
print*, "Pi = ", pi
print*, "e = ", e
end subroutine show_consts
end module constants
program module_example
use constants
implicit none
real :: x, ePowerx, area, radius
x = 2.0
radius = 7.0
ePowerx = e ** x
area = pi * radius**2
call show_consts()
print*, "e raised to the power of 2.0 = ", ePowerx
print*, "Area of a circle with radius 7.0 = ", area
end program module_example
When you compile and execute the above program, it gives the following error message −
ePowerx = e ** x 1 Error: Symbol 'e' at (1) has no IMPLICIT type main.f95:19.13: area = pi * radius**2 1 Error: Symbol 'pi' at (1) has no IMPLICIT type
Since e and pi, both are declared private, the program module_example cannot access these variables anymore.
However, other module subroutines can access them −
module constants
implicit none
real, parameter,private :: pi = 3.1415926536
real, parameter, private :: e = 2.7182818285
contains
subroutine show_consts()
print*, "Pi = ", pi
print*, "e = ", e
end subroutine show_consts
function ePowerx(x)result(ePx)
implicit none
real::x
real::ePx
ePx = e ** x
end function ePowerx
function areaCircle(r)result(a)
implicit none
real::r
real::a
a = pi * r**2
end function areaCircle
end module constants
program module_example
use constants
implicit none
call show_consts()
Print*, "e raised to the power of 2.0 = ", ePowerx(2.0)
print*, "Area of a circle with radius 7.0 = ", areaCircle(7.0)
end program module_example
When you compile and execute the above program, it produces the following result −
Pi = 3.14159274 e = 2.71828175 e raised to the power of 2.0 = 7.38905573 Area of a circle with radius 7.0 = 153.938049
Fortran - Intrinsic Functions
Intrinsic functions are some common and important functions that are provided as a part of the Fortran language. We have already discussed some of these functions in the Arrays, Characters and String chapters.
Intrinsic functions can be categorised as −
- Numeric Functions
- Mathematical Functions
- Numeric Inquiry Functions
- Floating-Point Manipulation Functions
- Bit Manipulation Functions
- Character Functions
- Kind Functions
- Logical Functions
- Array Functions.
We have discussed the array functions in the Arrays chapter. In the following section we provide brief descriptions of all these functions from other categories.
In the function name column,
- A represents any type of numeric variable
- R represents a real or integer variable
- X and Y represent real variables
- Z represents complex variable
- W represents real or complex variable
Numeric Functions
| Sr.No | Function & Description |
|---|---|
| 1 |
ABS (A) It returns the absolute value of A |
| 2 |
AIMAG (Z) It returns the imaginary part of a complex number Z |
| 3 |
AINT (A [, KIND]) It truncates fractional part of A towards zero, returning a real, whole number. |
| 4 |
ANINT (A [, KIND]) It returns a real value, the nearest integer or whole number. |
| 5 |
CEILING (A [, KIND]) It returns the least integer greater than or equal to number A. |
| 6 |
CMPLX (X [, Y, KIND]) It converts the real variables X and Y to a complex number X+iY; if Y is absent, 0 is used. |
| 7 |
CONJG (Z) It returns the complex conjugate of any complex number Z. |
| 8 |
DBLE (A) It converts A to a double precision real number. |
| 9 |
DIM (X, Y) It returns the positive difference of X and Y. |
| 10 |
DPROD (X, Y) It returns the double precision real product of X and Y. |
| 11 |
FLOOR (A [, KIND]) It provides the greatest integer less than or equal to number A. |
| 12 |
INT (A [, KIND]) It converts a number (real or integer) to integer, truncating the real part towards zero. |
| 13 |
MAX (A1, A2 [, A3,...]) It returns the maximum value from the arguments, all being of same type. |
| 14 |
MIN (A1, A2 [, A3,...]) It returns the minimum value from the arguments, all being of same type. |
| 15 |
MOD (A, P) It returns the remainder of A on division by P, both arguments being of the same type (A-INT(A/P)*P) |
| 16 |
MODULO (A, P) It returns A modulo P: (A-FLOOR(A/P)*P) |
| 17 |
NINT (A [, KIND]) It returns the nearest integer of number A |
| 18 |
REAL (A [, KIND]) It Converts to real type |
| 19 |
SIGN (A, B) It returns the absolute value of A multiplied by the sign of P. Basically it transfers the of sign of B to A. |
Example
program numericFunctions
implicit none
! define constants
! define variables
real :: a, b
complex :: z
! values for a, b
a = 15.2345
b = -20.7689
write(*,*) 'abs(a): ',abs(a),' abs(b): ',abs(b)
write(*,*) 'aint(a): ',aint(a),' aint(b): ',aint(b)
write(*,*) 'ceiling(a): ',ceiling(a),' ceiling(b): ',ceiling(b)
write(*,*) 'floor(a): ',floor(a),' floor(b): ',floor(b)
z = cmplx(a, b)
write(*,*) 'z: ',z
end program numericFunctions
When you compile and execute the above program, it produces the following result −
abs(a): 15.2344999 abs(b): 20.7688999 aint(a): 15.0000000 aint(b): -20.0000000 ceiling(a): 16 ceiling(b): -20 floor(a): 15 floor(b): -21 z: (15.2344999, -20.7688999)
Mathematical Functions
| Sr.No | Function & Description |
|---|---|
| 1 |
ACOS (X) It returns the inverse cosine in the range (0, ), in radians. |
| 2 |
ASIN (X) It returns the inverse sine in the range (-/2, /2), in radians. |
| 3 |
ATAN (X) It returns the inverse tangent in the range (-/2, /2), in radians. |
| 4 |
ATAN2 (Y, X) It returns the inverse tangent in the range (-, ), in radians. |
| 5 |
COS (X) It returns the cosine of argument in radians. |
| 6 |
COSH (X) It returns the hyperbolic cosine of argument in radians. |
| 7 |
EXP (X) It returns the exponential value of X. |
| 8 |
LOG (X) It returns the natural logarithmic value of X. |
| 9 |
LOG10 (X) It returns the common logarithmic (base 10) value of X. |
| 10 |
SIN (X) It returns the sine of argument in radians. |
| 11 |
SINH (X) It returns the hyperbolic sine of argument in radians. |
| 12 |
SQRT (X) It returns square root of X. |
| 13 |
TAN (X) It returns the tangent of argument in radians. |
| 14 |
TANH (X) It returns the hyperbolic tangent of argument in radians. |
Example
The following program computes the horizontal and vertical position x and y respectively of a projectile after a time, t −
Where, x = u t cos a and y = u t sin a - g t2 / 2
program projectileMotion implicit none ! define constants real, parameter :: g = 9.8 real, parameter :: pi = 3.1415927 !define variables real :: a, t, u, x, y !values for a, t, and u a = 45.0 t = 20.0 u = 10.0 ! convert angle to radians a = a * pi / 180.0 x = u * cos(a) * t y = u * sin(a) * t - 0.5 * g * t * t write(*,*) 'x: ',x,' y: ',y end program projectileMotion
When you compile and execute the above program, it produces the following result −
x: 141.421356 y: -1818.57861
Numeric Inquiry Functions
These functions work with a certain model of integer and floating-point arithmetic. The functions return properties of numbers of the same kind as the variable X, which can be real and in some cases integer.
| Sr.No | Function & Description |
|---|---|
| 1 |
DIGITS (X) It returns the number of significant digits of the model. |
| 2 |
EPSILON (X) It returns the number that is almost negligible compared to one. In other words, it returns the smallest value such that REAL( 1.0, KIND(X)) + EPSILON(X) is not equal to REAL( 1.0, KIND(X)). |
| 3 |
HUGE (X) It returns the largest number of the model |
| 4 |
MAXEXPONENT (X) It returns the maximum exponent of the model |
| 5 |
MINEXPONENT (X) It returns the minimum exponent of the model |
| 6 |
PRECISION (X) It returns the decimal precision |
| 7 |
RADIX (X) It returns the base of the model |
| 8 |
RANGE (X) It returns the decimal exponent range |
| 9 |
TINY (X) It returns the smallest positive number of the model |
Floating-Point Manipulation Functions
| Sr.No | Function & Description |
|---|---|
| 1 |
EXPONENT (X) It returns the exponent part of a model number |
| 2 |
FRACTION (X) It returns the fractional part of a number |
| 3 |
NEAREST (X, S) It returns the nearest different processor number in given direction |
| 4 |
RRSPACING (X) It returns the reciprocal of the relative spacing of model numbers near given number |
| 5 |
SCALE (X, I) It multiplies a real by its base to an integer power |
| 6 |
SET_EXPONENT (X, I) it returns the exponent part of a number |
| 7 |
SPACING (X) It returns the absolute spacing of model numbers near given number |
Bit Manipulation Functions
| Sr.No | Function & Description |
|---|---|
| 1 |
BIT_SIZE (I) It returns the number of bits of the model |
| 2 |
BTEST (I, POS) Bit testing |
| 3 |
IAND (I, J) Logical AND |
| 4 |
IBCLR (I, POS) Clear bit |
| 5 |
IBITS (I, POS, LEN) Bit extraction |
| 6 |
IBSET (I, POS) Set bit |
| 7 |
IEOR (I, J) Exclusive OR |
| 8 |
IOR (I, J) Inclusive OR |
| 9 |
ISHFT (I, SHIFT) Logical shift |
| 10 |
ISHFTC (I, SHIFT [, SIZE]) Circular shift |
| 11 |
NOT (I) Logical complement |
Character Functions
| Sr.No | Function & Description |
|---|---|
| 1 |
ACHAR (I) It returns the Ith character in the ASCII collating sequence. |
| 2 |
ADJUSTL (STRING) It adjusts string left by removing any leading blanks and inserting trailing blanks |
| 3 |
ADJUSTR (STRING) It adjusts string right by removing trailing blanks and inserting leading blanks. |
| 4 |
CHAR (I [, KIND]) It returns the Ith character in the machine specic collating sequence |
| 5 |
IACHAR (C) It returns the position of the character in the ASCII collating sequence. |
| 6 |
ICHAR (C) It returns the position of the character in the machine (processor) specic collating sequence. |
| 7 |
INDEX (STRING, SUBSTRING [, BACK]) It returns the leftmost (rightmost if BACK is .TRUE.) starting position of SUBSTRING within STRING. |
| 8 |
LEN (STRING) It returns the length of a string. |
| 9 |
LEN_TRIM (STRING) It returns the length of a string without trailing blank characters. |
| 10 |
LGE (STRING_A, STRING_B) Lexically greater than or equal |
| 11 |
LGT (STRING_A, STRING_B) Lexically greater than |
| 12 |
LLE (STRING_A, STRING_B) Lexically less than or equal |
| 13 |
LLT (STRING_A, STRING_B) Lexically less than |
| 14 |
REPEAT (STRING, NCOPIES) Repeated concatenation |
| 15 |
SCAN (STRING, SET [, BACK]) It returns the index of the leftmost (rightmost if BACK is .TRUE.) character of STRING that belong to SET, or 0 if none belong. |
| 16 |
TRIM (STRING) Removes trailing blank characters |
| 17 |
VERIFY (STRING, SET [, BACK]) Verifies the set of characters in a string |
Kind Functions
| Sr.No | Function & Description |
|---|---|
| 1 |
KIND (X) It returns the kind type parameter value. |
| 2 |
SELECTED_INT_KIND (R) It returns kind of type parameter for specied exponent range. |
| 3 |
SELECTED_REAL_KIND ([P, R]) Real kind type parameter value, given precision and range |
Logical Function
| Sr.No | Function & Description |
|---|---|
| 1 |
LOGICAL (L [, KIND]) Convert between objects of type logical with different kind type parameters |
Fortran - Numeric Precision
We have already discussed that, in older versions of Fortran, there were two real types: the default real type and double precision type.
However, Fortran 90/95 provides more control over the precision of real and integer data types through the kind specifie.
The Kind Attribute
Different kind of numbers are stored differently inside the computer. The kind attribute allows you to specify how a number is stored internally. For example,
real, kind = 2 :: a, b, c real, kind = 4 :: e, f, g integer, kind = 2 :: i, j, k integer, kind = 3 :: l, m, n
In the above declaration, the real variables e, f and g have more precision than the real variables a, b and c. The integer variables l, m and n, can store larger values and have more digits for storage than the integer variables i, j and k. Although this is machine dependent.
Example
program kindSpecifier implicit none real(kind = 4) :: a, b, c real(kind = 8) :: e, f, g integer(kind = 2) :: i, j, k integer(kind = 4) :: l, m, n integer :: kind_a, kind_i, kind_e, kind_l kind_a = kind(a) kind_i = kind(i) kind_e = kind(e) kind_l = kind(l) print *,'default kind for real is', kind_a print *,'default kind for int is', kind_i print *,'extended kind for real is', kind_e print *,'default kind for int is', kind_l end program kindSpecifier
When you compile and execute the above program it produces the following result −
default kind for real is 4 default kind for int is 2 extended kind for real is 8 default kind for int is 4
Inquiring the Size of Variables
There are a number of intrinsic functions that allows you to interrogate the size of numbers.
For example, the bit_size(i) intrinsic function specifies the number of bits used for storage. For real numbers, the precision(x) intrinsic function, returns the number of decimal digits of precision, while the range(x) intrinsic function returns the decimal range of the exponent.
Example
program getSize implicit none real (kind = 4) :: a real (kind = 8) :: b integer (kind = 2) :: i integer (kind = 4) :: j print *,'precision of real(4) =', precision(a) print *,'precision of real(8) =', precision(b) print *,'range of real(4) =', range(a) print *,'range of real(8) =', range(b) print *,'maximum exponent of real(4) =' , maxexponent(a) print *,'maximum exponent of real(8) =' , maxexponent(b) print *,'minimum exponent of real(4) =' , minexponent(a) print *,'minimum exponent of real(8) =' , minexponent(b) print *,'bits in integer(2) =' , bit_size(i) print *,'bits in integer(4) =' , bit_size(j) end program getSize
When you compile and execute the above program it produces the following result −
precision of real(4) = 6 precision of real(8) = 15 range of real(4) = 37 range of real(8) = 307 maximum exponent of real(4) = 128 maximum exponent of real(8) = 1024 minimum exponent of real(4) = -125 minimum exponent of real(8) = -1021 bits in integer(2) = 16 bits in integer(4) = 32
Obtaining the Kind Value
Fortran provides two more intrinsic functions to obtain the kind value for the required precision of integers and reals −
- selected_int_kind (r)
- selected_real_kind ([p, r])
The selected_real_kind function returns an integer that is the kind type parameter value necessary for a given decimal precision p and decimal exponent range r. The decimal precision is the number of significant digits, and the decimal exponent range specifies the smallest and largest representable number. The range is thus from 10-r to 10+r.
For example, selected_real_kind (p = 10, r = 99) returns the kind value needed for a precision of 10 decimal places, and a range of at least 10-99 to 10+99.
Example
program getKind implicit none integer:: i i = selected_real_kind (p = 10, r = 99) print *,'selected_real_kind (p = 10, r = 99)', i end program getKind
When you compile and execute the above program it produces the following result −
selected_real_kind (p = 10, r = 99) 8
Fortran - Program Libraries
There are various Fortran tools and libraries. Some are free and some are paid services.
Following are some free libraries −
- RANDLIB, random number and statistical distribution generators
- BLAS
- EISPACK
- GAMSNIST Guide to Available Math Software
- Some statistical and other routines from NIST
- LAPACK
- LINPACK
- MINPACK
- MUDPACK
- NCAR Mathematical Library
- The Netlib collection of mathematical software, papers, and databases.
- ODEPACK
- ODERPACK, a set of routines for ranking and ordering.
- Expokit for computing matrix exponentials
- SLATEC
- SPECFUN
- STARPAC
- StatLib statistical library
- TOMS
- Sorting and merging strings
The following libraries are not free −
- The NAG Fortran numerical library
- The Visual Numerics IMSL library
- Numerical Recipes
Fortran - Programming Style
Programming style is all about following some rules while developing programs. These good practices impart values like readability, and unambiguity into your program.
A good program should have the following characteristics −
- Readability
- Proper logical structure
- Self-explanatory notes and comments
For example, if you make a comment like the following, it will not be of much help −
! loop from 1 to 10 do i = 1,10
However, if you are calculating binomial coefficient, and need this loop for nCr then a comment like this will be helpful −
! loop to calculate nCr do i = 1,10
Indented code blocks to make various levels of code clear.
Self-checking codes to ensure there will be no numerical errors like division by zero, square root of a negative real number or logarithm of a negative real number.
Including codes that ensure variables do not take illegal or out of range values, i.e., input validation.
Not putting checks where it would be unnecessary and slows down the execution. For example −
real :: x x = sin(y) + 1.0 if (x >= 0.0) then z = sqrt(x) end if
- Clearly written code using appropriate algorithms.
- Splitting the long expressions using the continuation marker &.
- Making meaningful variable names.
Fortran - Debugging Program
A debugger tool is used to search for errors in the programs.
A debugger program steps through the code and allows you to examine the values in the variables and other data objects during execution of the program.
It loads the source code and you are supposed to run the program within the debugger. Debuggers debug a program by −
- Setting breakpoints,
- Stepping through the source code,
- Setting watch points.
Breakpoints specify where the program should stop, specifically after a critical line of code. Program executions after the variables are checked at a breakpoint.
Debugger programs also check the source code line by line.
Watch points are the points where the values of some variables are needed to be checked, particularly after a read or write operation.
The gdb Debugger
The gdb debugger, the GNU debugger comes with Linux operating system. For X windows system, gdb comes with a graphical interface and the program is named xxgdb.
Following table provides some commands in gdb −
| Command | Purpose |
|---|---|
| break | Setting a breakpoint |
| run | Starts execution |
| cont | Continues execution |
| next | Executes only the next line of source code, without stepping into any function call |
| step | Execute the next line of source code by stepping into a function in case of a function call. |
The dbx Debugger
There is another debugger, the dbx debugger, for Linux.
The following table provides some commands in dbx −
| Command | Purpose |
|---|---|
| stop[var] | Sets a breakpoint when the value of variable var changes. |
| stop in [proc] | It stops execution when a procedure proc is entered |
| stop at [line] | It sets a breakpoint at a specified line. |
| run | Starts execution. |
| cont | Continues execution. |
| next | Executes only the next line of source code, without stepping into any function call. |
| step | Execute the next line of source code by stepping into a function in case of a function call. |