Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find the City With the Smallest Number of Neighbors at a Threshold Distance in C++
Suppose there are n cities numbered from 0 to n-1. If we have the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distance threshold. We have to find the city with the smallest number of cities that are reachable through some path and whose distance is at most distance threshold, If there are more than one such cities, return the city with the greatest number.
So if the input is like −
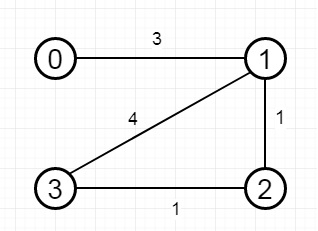
n is 4 and the distance threshold is also 4, then the output will be 3. This is because −
The neighboring cities at a distance threshold = 4 for each city are −
C0 -> [C1, C2] C1 -> [C0, C2, C3] C2 -> [C0, C1, C3] C3 -> [C1, C2]
Cities 0 and 3 have 2 neighboring cities at a distance threshold = 4, but we have to return city 3 since it has the greatest number.
To solve this, we will follow these steps −
Define a square matrix of order n x n called dp and fill this with infinity
generate the adjacency matrix (cost matrix) of the graph and store into dp
ret := 0 and cnt := infinity
for k in range 0 to n – 1
for i in range 0 to n – 1
for j in range 0 to n – 1
if i = j, then go for next iteration
if dp[i, j] > dp[i, k] + dp[k, j], then
dp[j, i] := dp[i, k] + dp[k, j]
dp[i, j] := dp[i, k] + dp[k, j]
for i in range 0 to n - 1
temp := 0
for j in range 0 to n – 1
temp := temp + 1 when dp[i, j] <= t, otherwise temp remains same
if temp <= cnt, then cnt := temp and ret := i
return ret
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int findTheCity(int n, vector<vector<int>>& e, int t) {
vector < vector <int> > dp(n, vector <int>(n, 1e7));
for(int i = 0; i < e.size(); i++){
int u = e[i][0];
int v = e[i][1];
int w = e[i][2];
dp[u][v] = w;
dp[v][u] = w;
}
int ret = 0;
int cnt = INT_MAX;
for(int k = 0; k < n; k++){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
if(i == j) continue;
if(dp[i][j] > dp[i][k] + dp[k][j]){
dp[j][i] = dp[i][j] = (dp[i][k] + dp[k][j]);
}
}
}
}
for(int i = 0; i < n; i++){
int temp = 0;
for(int j = 0; j < n; j++){
temp += (dp[i][j] <= t);
}
if(temp <= cnt){
cnt = temp;
ret = i;
}
}
return ret;
}
};
main(){
vector<vector<int>> v = {{0,1,3},{1,2,1},{1,3,4},{2,3,1}};
Solution ob;
cout << (ob.findTheCity(4, v, 4));
}Input
4 [[0,1,3],[1,2,1],[1,3,4],[2,3,1]] 4
Output
3
394 Views
