Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find if there is a triplet in a Balanced BST that adds to zero in C++
Suppose we have a balanced binary search tree, we have to create a function named is_valid_triplet() that returns true when there exist a triplet in given BST whose sum equals to 0, otherwise returns false. Design the method by following these constraints −
expected time complexity is O(n^2)
O(logn) extra space can be used.
So, if the input is like
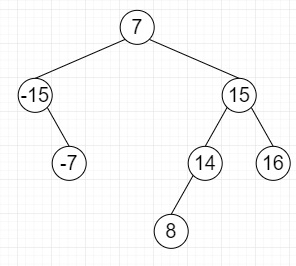
then the output will be True, as triplet is [-15,7,8]
To solve this, we will follow these steps −
Define a function bst_to_doubli_list(), this will take root, head, tail,
if root is same as NULL, then −
return
if left of root is not null, then −
bst_to_doubli_list(left of root, head, tail)
left of root := tail
if tail is not null , then −
right of tail := root
Otherwise
head := root
tail := root
if right of root is not null, then −
bst_to_doubli_list(right of root, head, tail)
Define a function is_in_double_list(), this will take head, tail, sum,
while head is not equal to tail, do −
current := key of head + key of tail
if current is same as sum, then −
return true
otherwise when current > sum, then −
tail := left of tail
Otherwise
head := right of head
return false
From the main method, do the following −
if root is null, then −
return false
head = null
tail = null
bst_to_doubli_list(root, head, tail)
while (right of head is not equal to tail and key of head < 0), do −
if is_in_double(right of head, tail, key of head * (-1), then
return true
Otherwise
head := right of head
return false
Example (C++)
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int key;
TreeNode *left;
TreeNode *right;
TreeNode() : key(0), left(NULL), right(NULL) {}
TreeNode(int x) : key(x), left(NULL), right(NULL) {}
};
void bst_to_doubli_list(TreeNode* root, TreeNode** head, TreeNode** tail) {
if (root == NULL)
return;
if (root->left)
bst_to_doubli_list(root->left, head, tail);
root->left = *tail;
if (*tail)
(*tail)->right = root;
else
*head = root;
*tail = root;
if (root->right)
bst_to_doubli_list(root->right, head, tail);
}
bool is_in_double_list(TreeNode* head, TreeNode* tail, int sum) {
while (head != tail) {
int current = head->key + tail->key;
if (current == sum)
return true;
else if (current > sum)
tail = tail->left;
else
head = head->right;
}
return false;
}
bool is_valid_triplet(TreeNode *root) {
if (root == NULL)
return false;
TreeNode* head = NULL;
TreeNode* tail = NULL;
bst_to_doubli_list(root, &head, &tail);
while ((head->right != tail) && (head->key < 0)){
if (is_in_double_list(head->right, tail, -1*head->key))
return true;
else
head = head->right;
}
return false;
}
TreeNode* insert(TreeNode* root, int key) {
if (root == NULL)
return new TreeNode(key);
if (root->key > key)
root->left = insert(root->left, key);
else
root->right = insert(root->right, key);
return root;
}
int main(){
TreeNode* root = NULL;
root = insert(root, 7);
root = insert(root, -15);
root = insert(root, 15);
root = insert(root, -7);
root = insert(root, 14);
root = insert(root, 16);
root = insert(root, 8);
cout << is_valid_triplet(root);
}Input
root = insert(root, 7); root = insert(root, -15); root = insert(root, 15); root = insert(root, -7); root = insert(root, 14); root = insert(root, 16); root = insert(root, 8);
Output
1
137 Views
