Find a pair with given sum in a Balanced BST in Java

Concept

With respect of a given Balanced Binary Search Tree and a target sum, we write a function that returns true if there is a pair with sum equals to target sum, otherwise return false. In this case, expected time complexity is O(n) and only O(Logn) extra space can beimplemented. Here, any modification to Binary Search Tree is not permitted.We have to note that height of a Balanced BST is always O(Logn).

Example

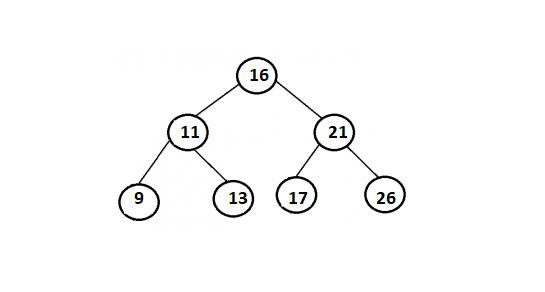
Method

According to the Brute Force Solution, we consider each pair in BST and verify whether the sum equals to X. The time complexity of this solution will be O(n^2).

Now a better solution is to build an auxiliary array and store Inorder traversal of BST in the array. In this case, the array will be sorted as inorder traversal of BST always produces sorted data. So once after availability of the inorder traversal, we can pair in O(n) time. Remember, this solution works in O(n) time, but requires O(n) auxiliary space.

Example

 Live Demo

// Java code to find a pair with given sum
// in a Balanced BST
import java.util.ArrayList;
// A binary tree node
class Node1 {
   int data1;
   Node1 left1, right1;
   Node1(int d){
      data1 = d;
      left1 = right1 = null;
   }
}
public class BinarySearchTree {
   // Indicates root of BST
   Node1 root1;
   // Indicates constructor
   BinarySearchTree(){
      root1 = null;
   }
   // Indicates inorder traversal of the tree
   void inorder(){
      inorderUtil1(this.root1);
   }
   // Indicates utility function for inorder traversal of the tree
   void inorderUtil1(Node1 node1){
      if (node1 == null)
         return;
      inorderUtil1(node1.left1);
      System.out.print(node1.data1 + " ");
      inorderUtil1(node1.right1);
   }
   // Now this method mainly calls insertRec()
   void insert(int key1){
      root1 = insertRec1(root1, key1);
   }
   /* Indicates a recursive function to insert a new key in BST */
   Node1 insertRec1(Node1 root1, int data1){
   /* So if the tree is empty, return a new node */
   if (root1 == null) {
      root1 = new Node1(data1);
      return root1;
   }
   /* Otherwise, recur down the tree */
   if (data1 < root1.data1)
      root1.left1 = insertRec1(root1.left1, data1);
   else if (data1 > root1.data1)
      root1.right1 = insertRec1(root1.right1, data1);
   return root1;
}
// Indicates method that adds values of given BST into ArrayList
// and hence returns the ArrayList
ArrayList<Integer> treeToList(Node1 node1, ArrayList<Integer> list1){
   // Indicates Base Case
   if (node1 == null)
      return list1;
   treeToList(node1.left1, list1);
   list1.add(node1.data1);
   treeToList(node1.right1, list1);
   return list1;
}
// Indicates method that checks if there is a pair present
boolean isPairPresent(Node1 node1, int target1){
   // Now this list a1 is passed as an argument
   // in treeToList method
   // which is later on filled by the values of BST
   ArrayList<Integer> a1 = new ArrayList<>();
   // Now a2 list contains all the values of BST
   // returned by treeToList method
   ArrayList<Integer> a2 = treeToList(node1, a1);
   int start1 = 0; // Indicates starting index of a2
   int end1 = a2.size() - 1; // Indicates ending index of a2
   while (start1 < end1) {
      if (a2.get(start1) + a2.get(end1) == target1) // Target Found!{
         System.out.println("Pair Found: " + a2.get(start1) + " + " + a2.get(end1) + " " + "= " + target1);
         return true;
      }
      if (a2.get(start1) + a2.get(end1) > target1)
      // decrements end
      {
         end1--;
      }
      if (a2.get(start1) + a2.get(end1) < target1)
      // increments start
      {
         start1++;
      }
   }
   System.out.println("No such values are found!");
   return false;
}
// Driver function
public static void main(String[] args){
   BinarySearchTree tree1 = new BinarySearchTree();
/*
   16
   / \
  11 21
 / \ / \
9 13 17 26 */
      tree1.insert(16);
      tree1.insert(11);
      tree1.insert(21);
      tree1.insert(9);
      tree1.insert(13);
      tree1.insert(17);
      tree1.insert(26);
      tree1.isPairPresent(tree1.root1, 34);
   }
}

Output

Pair Found: 13 + 21 = 34