Fill 8 numbers in grid with given conditions in C++

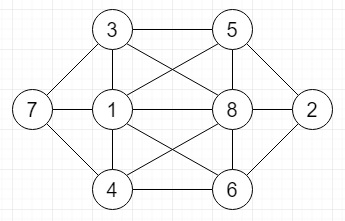
Suppose we want to place 1, 2, 3, 4, 5, 6, 7, 8, into the eight circles in the given figure, in this way that no number is adjacent to a number that is next to it in the sequence.

So, if the input is like

0	- 1	- 1	0
- 1	- 1	- 1	- 1
0	- 1	- 1	0

then the output will be

To solve this, we will follow these steps −

• N := 3, M := 4
• NOTCONSIDERED := -1
• Define a function present_in_grid(), this will take grid[N][M], num,
• for initialize i := 0, when i < N, update (increase i by 1), do:
  • for initialize j := 0, when j < M, update (increase j by 1), do −
    • if grid[i, j] is same as num, then −
      • return true
• return false
• Define a function isSafe(), this will take grid[N][M], row, col, num,
• if row is same as 0 and col is same as 1, then −
  • if present_in_grid(grid, num) or |num - grid[row, col + 1]| <= 1 or |num - grid[row + 1, col]| <= 1 or |num - grid[row + 1, col - 1]| <= 1 or |num - grid[row + 1, col + 1]| <= 1, then −
    • return false
• otherwise when row is same as 0 and col is same as 2, then −
  • if present_in_grid(grid, num) or |num - grid[row, col - 1]| <= 1 or |num - grid[row + 1, col]| <= 1 or |num - grid[row + 1, col + 1]| <= 1 or |num - grid[row + 1, col - 1]| <= 1, then −
    • return false
• otherwise when row is same as 1 and col is same as 0, then −
  • if present_in_grid(grid, num) or |num - grid[row - 1, col + 1]| <= 1 or |num - grid[row, col + 1]| <= 1 or |num - grid[row + 1, col + 1]| <= 1, then −
  • return false
• otherwise when row is same as 1 and col is same as 3, then −
  • if present_in_grid(grid, num) or |num - grid[row - 1, col - 1]| <= 1 or |num - grid[row, col - 1]| <= 1 or |num - grid[row + 1, col - 1]| <= 1, then −
    • return false
• otherwise when row is same as 2 and col is same as 1, then −
  • if present_in_grid(grid, num) or |num - grid[row - 1, col - 1]| <= 1 or |num - grid[row - 1, col]| <= 1 or |num - grid[row - 1, col + 1]| <= 1 or |num - grid[row, col + 1]| <= 1, then −
    • return false
• otherwise when row is same as 2 and col is same as 2, then −
  • if present_in_grid(grid, num) or |num - grid[row, col - 1]| <= 1 or |num - grid[row - 1, col]| <= 1 or |num - grid[row - 1, col + 1]| <= 1 or |num - grid[row - 1, col - 1]| <= 1, then −
    • return false
• otherwise when row is same as 1 and col is same as 1, then −
  • if present_in_grid(grid, num) or |num - grid[row, col - 1]| <= 1 or |num - grid[row - 1, col]| <= 1 or |num - grid[row - 1, col + 1]| <= 1 or |num - grid[row, col + 1]| <= 1 or |num - grid[row + 1, col + 1]| <= 1 or |num - grid[row + 1, col]| <= 1, then −
    • return false
• otherwise when row is same as 1 and col is same as 2, then −
  • if present_in_grid(grid, num) or |num - grid[row, col - 1]| <= 1 or |num - grid[row - 1, col]| <= 1 or |num - grid[row + 1, col - 1]| <= 1 or |num - grid[row, col + 1]| <= 1 or |num - grid[row - 1, col - 1]| <= 1 or |num - grid[row + 1, col]| 1, then −
    • return false
• return true
• Define a function search_free_location(), this will take grid[N][M], row, col,
  • for initialize row := 0, when row < N, update (increase row by 1), do −
    • for initialize col := 0, when col < M, update (increase col by 1), do −
    • if grid[row, col] is same as NOTCONSIDERED, then −
      • return true
• return false
• Define a function Solve(), this will take grid[N][M],
• if search_free_location(grid, row, col) is false, then −
  • return true
• for initialize num := 1, when num <= 8, update (increase num by 1), do −
  • if isSafe(grid, row, col, num), then −
    • grid[row, col] := num
    • if Solve(grid) is true, then −
      • return true
  • grid[row, col] := NOTCONSIDERED
• return false

Example

Let us see the following implementation to get better understanding −

 Live Demo

#include <cmath>
#include <iostream>
#define N 3
#define M 4
#define NOTCONSIDERED -1
using namespace std;
bool present_in_grid(int grid[N][M], int num) {
   for (int i = 0; i < N; i++) {
      for (int j = 0; j < M; j++)
         if (grid[i][j] == num)
            return true;
   }
   return false;
}
bool isSafe(int grid[N][M], int row, int col, int num) {
   if (row == 0 && col == 1) {
      if (present_in_grid(grid, num) || (abs(num - grid[row][col + 1]) <= 1) || (abs(num - grid[row + 1][col]) <= 1) || (abs(num - grid[row + 1][col - 1]) <= 1) || (abs(num - grid[row + 1][col + 1]) <= 1))
         return false;
   }
   else if (row == 0 && col == 2) {
      if (present_in_grid(grid, num) || (abs(num - grid[row][col - 1]) <= 1) || (abs(num - grid[row + 1][col]) <= 1) || (abs(num - grid[row + 1][col + 1]) <= 1) || (abs(num - grid[row + 1][col - 1]) <= 1))
         return false;
   }
   else if (row == 1 && col == 0) {
      if (present_in_grid(grid, num) || (abs(num - grid[row - 1][col + 1]) <= 1) || (abs(num - grid[row][col + 1]) <= 1) || (abs(num - grid[row + 1][col + 1]) <= 1))
         return false;
   }
   else if (row == 1 && col == 3) {
      if (present_in_grid(grid, num) || (abs(num - grid[row - 1][col - 1]) <= 1) || (abs(num - grid[row][col - 1]) <= 1) || (abs(num - grid[row + 1][col - 1]) <= 1))
         return false;
   }
   else if (row == 2 && col == 1) {
   if (present_in_grid(grid, num) || (abs(num - grid[row - 1][col - 1]) <= 1) || (abs(num - grid[row - 1][col]) <= 1) || (abs(num - grid[row - 1][col + 1]) <= 1) || (abs(num - grid[row][col + 1]) <= 1))
      return false;
   }
   else if (row == 2 && col == 2) {
      if (present_in_grid(grid, num) || (abs(num - grid[row][col - 1]) <= 1) || (abs(num - grid[row - 1][col]) <= 1) || (abs(num - grid[row - 1][col + 1]) <= 1) || (abs(num - grid[row - 1][col - 1]) <= 1))
         return false;
   }
   else if (row == 1 && col == 1) {
      if (present_in_grid(grid, num) || (abs(num - grid[row][col - 1]) <= 1) || (abs(num - grid[row - 1][col]) <= 1) || (abs(num - grid[row - 1][col + 1]) <= 1) || (abs(num - grid[row][col + 1]) <= 1) || (abs(num - grid[row + 1][col + 1]) <= 1) || (abs(num - grid[row + 1][col]) <= 1))
         return false;
   }
   else if (row == 1 && col == 2) {
      if (present_in_grid(grid, num) || (abs(num - grid[row][col - 1]) <= 1) || (abs(num - grid[row - 1][col]) <= 1) || (abs(num - grid[row + 1][col - 1]) <= 1) || (abs(num - grid[row][col + 1]) <= 1) || (abs(num - grid[row - 1][col - 1]) <= 1) || (abs(num - grid[row + 1][col]) <= 1))
         return false;
   }
   return true;
}
bool search_free_location(int grid[N][M], int& row, int& col) {
   for (row = 0; row < N; row++)
   for (col = 0; col < M; col++) {
      if (grid[row][col] == NOTCONSIDERED)
         return true;
   }
   return false;
}
void show_res(int grid[N][M]) {
   for (int i = 0; i < N; i++) {
      if (i == 0 || i == N - 1)
         cout << " ";
      for (int j = 0; j < M; j++) {
         if (grid[i][j] == 0)
            cout << " ";
         else
            cout << grid[i][j] << " ";
      }
      cout << endl;
   }
}
bool Solve(int grid[N][M]) {
   int row, col;
   if (!search_free_location(grid, row, col))
   return true;
   for (int num = 1; num <= 8; num++) {
      if (isSafe(grid, row, col, num)) {
         grid[row][col] = num;
         if (Solve(grid))
            return true;
         grid[row][col] = NOTCONSIDERED;
      }
   }
   return false;
}
int main(){
   int grid[N][M] = { { 0, -1, -1, 0 },
      { -1, -1, -1, -1 },
      { 0, -1, -1, 0 } };
   if (Solve(grid))
      show_res(grid);
   else
      cout << "Not possible";
}

Input

{ { 0, -1, -1, 0 },
{ -1, -1, -1, -1},
{ 0, -1, -1, 0 }}

Output

  3 5
7 1 8 2
  4 6