FIFO Push Relabel Algorithm

The FIFO Push Relabel algorithm is an algorithm that is used to solve the maximum flow problem.

The maximum flow problem is a problem in graph theory in which we have to find the maximum amount of flow of resources or information that can be sent via an interconnected network of components, like pipes, wires, etc. With constraints on how much capacity a single component can handle.

In other words, we have a directed graph on N nodes. We are given a source node and a sink node. We also have M edges in the graph, each edge has a weight assigned to it, which represents the maximum amount of capacity it can handle. We need to figure out the maximum amount of flow that can be transferred from the source node to the sink node without exceeding the capacity of any of the edges.

In the first approach, we are given a directed graph G, representing the edges of the flow network. Each edge has a weight assigned to it, which represents the maximum capacity of the respective edge. We initialize the flow on every edge to be zero at the start. We repeatedly check if we can transfer the information from source node to sink node by doing a breadth-first search. Till there is a way to transfer information from the source to the sink, we transfer that amount of information and add it to the final answer. We also subtract it from the capacity of each of the edges involved.

Problem Statement

Given a flow network in the form of a directed graph G, and the weights of the edges representing the maximum capacity of each edge. We need to find the maximum flow we can transfer from the source node to the sink node such that −

• No edge has a load that exceeds its capacity.

• The sum of all incoming edges to a node is equal to the sum of all outgoing edges.

Sample Examples

Input

Source = 1, Sink = 4

Output

10

Explanation

We can flow 10 units from 1 to 2, and since the incoming and outgoing edges must have the same sum, we can only move 10 units from 2 to 3, and also from 3 to 4

Input

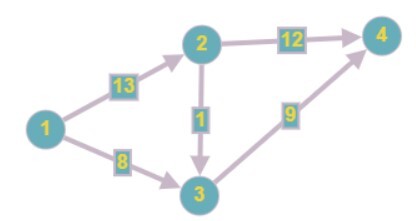
Source = 1, Sink = 4

Output

21

Explanation

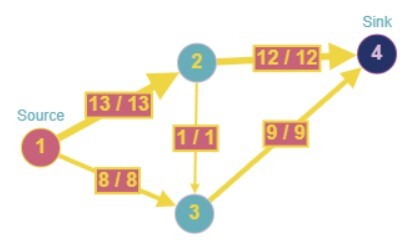
Input

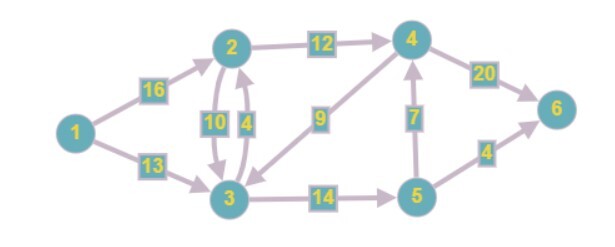
Source = 1, Sink = 6

Output

23

Explanation

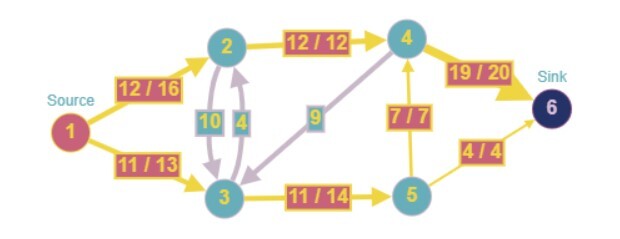
As shown in the above diagram, we can get the maximum flow of 23.

Since the sum of incoming edges must be equal to the outgoing edges and the sum of incoming edges at the vertex 4 is 19, we can only flow 19 units from the edge 4-6, even though the capacity of the edge is 20.

Approach

In this approach, we are given a directed graph G, representing the edges of the flow network. Each edge has a weight assigned to it, which represents the maximum capacity of the respective edge. We initialize the flow on every edge to be zero at the start. We repeatedly check if we can transfer the information from source node to sink node by doing a breadth-first search. Till there is a way to transfer information from the source to the sink, we transfer that amount of information and add it to the final answer. We also subtract it from the capacity of each of the edges involved.

Algorithm

• Step 1.1 − Set the initial flow on all edges to be zero.

• Step 1.2 − Assign the source node a height equal to the total number of nodes in the network.

• Step 1.3 − Calculate the excess flow at the source node, which is the sum of capacities of all edges emanating from it.

• Step 2.1 − At each node (excluding the source and sink), examine if there's excessive flow, greater than incoming flow, and a neighboring node with a height one less than the current node's height.

• Step 2.2 − If the above condition is true, push as much flow as possible along the edge, and update the excess flow at the current node and the overall capacity of the edge.

• Step 3.1 − If the above condition is false, then the height of that node needs to be increased.

• Step 3.2 − The new height of the node is calculated by adding one to the minimum height of its neighbor with current capacity greater than zero.

• Step 4.1 − Instead of repeatedly scanning all nodes for potential pushes and relabels, the algorithm utilizes a First-In-First-Out (FIFO) queue to systematically manage nodes for processing.

• Step 4.2 − After we check the condition mentioned in step 2.1, we push the neighboring nodes into the queue.

• Step 5 − The algorithm runs until no node in the network has any excessive flow from the source node. When this condition is met, the algorithm returns the maximum flow.

Example

#include <bits/stdc++.h>
using namespace std;
bool Can_push(vector<vector<int>> &Capacity, int source, int sink, vector<int> &parent) {
   int N = Capacity.size();
   vector<int> vis(N,0);
   vis[source]=1;
   parent[source]=-1;
   queue<int> que;
   que.push(source);
   while(!que.empty())    {
      int cnode = que.front();
      que.pop();
      for (int i=0;i<N;i++){
         if (vis[i]==0 && Capacity[cnode][i] > 0){
            vis[i] = 1;
            parent[i] = cnode;
            que.push(i);
         }
      }
   }
   if(vis[sink])return true;
   return false;
}
int FIFOPushRelabel(vector<vector<int>> &Capacity, int source, int sink){
   int N = Capacity.size();
   vector<int> parent(N);
   int max_flow = 0;
   while(Can_push(Capacity,source,sink,parent)){
      int curr_flow = INT_MAX;
      int temp = sink;
      while(temp!=source){
         curr_flow = min(curr_flow,Capacity[parent[temp]][temp]);
         temp = parent[temp];
      }
      temp = sink;
      while(temp!=source){
         Capacity[parent[temp]][temp]-=curr_flow;
         temp = parent[temp];
      }
      max_flow+=curr_flow;
   }
   return max_flow;
}
int main() {
   vector<vector<int>> Capacity = {
      {0, 16, 13, 0, 0, 0},
      {0, 0, 10, 12, 0, 0},
      {0, 4, 0, 0, 14, 0},
      {0, 0, 9, 0, 0, 20},
      {0, 0, 0, 7, 0, 4},
      {0, 0, 0, 0, 0, 0}
   };
   int source = 0, sink = 5;
   cout<<FIFOPushRelabel(Capacity,source,sink);
   return 0;
}

Output

23

Time complexity − O(V^3), where V is the number of nodes in the graph.

Space complexity − O(V^2), to store adjacency matrix representing the graph.