Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain the basic properties of the Turing machine?
Turing machines are more powerful than both finite automata (FA) and pushdown automata (PDA). They are as powerful as any computer we have ever built.
The main improvements from PDAs in Turing machine are explained below −
Infinite “all” accessible memory (in the form of a tape) – option to read and write to it.
A read/write head can move to the left and to the right on the input tape (or don’t change a position).
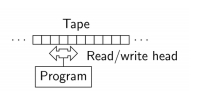
The TM works on an infinite tape divided into cells (infinite in both directions), each of which contains either a symbol from an alphabet or the blank symbol. (Only a finite number of non-blank symbols are written on the tape.)
The TM is always in one of a finite number of states.
The read/write head reads the symbol in the “current cell” and depending on the symbol and the current state −
Change the state
Move the head in either direction or not move at all
Re-write the “current symbol” or leave it unchanged
By default we are talking about deterministic Turing machines.
Moving around the tape
At each step, there are three possible movements for the head, which are as follows −
“Move to left by one cell from the current cell,”
“Stay at the current cell,” or
“Move to right by one cell,”
We will represent these by the letters − L, S, and R.
Turing Machine instructions (transition functions)
Each Turing machine (TM) instruction contains five parts −
IN − The current machine state. (from Q)
IN − The tape symbol read from the current tape cell (may be the blank symbol) (from Γ )
OUT − A tape symbol to write into the current tape cell (may be the blank symbol or also other symbols) (from Γ )
OUT − The next machine state (from Q)
OUT − A direction for the tape head to move in {L, R, S}.
T : Q × Γ → Γ × Q × {L, R, S}
Two inputs, three outputs: T(i, a) = (b, j, R)
Γ contains ∑ (the alphabet of the language), ‘empty tape symbol’ –, but also other symbols.
The instruction in the graphical form is as follows −
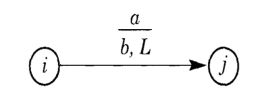
This means the same as before −
If the current state of the machine is i, and if the symbol in the current tape cell is a,
↓
Then, write b into the current tape cell, move left by one cell, and go to state j.
An input string is represented on the tape by placing the letters of the string (from ∑) into adjacent tape cells.
All other cells of the tape contain the blank symbol, which we will denote by .
The head is usually positioned over the leftmost cell of the input string (the leftmost non-blank tape symbol).
3K+ Views
