
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain NFA with epsilon transition.
We extend the class of NFAs by allowing instantaneous ε transitions −
The automaton may be allowed to change its state without reading the input symbol 2.
In diagrams, such transitions are depicted by labeling the appropriate arcs with ε.
Note that this does not mean that E has become an input symbol. On the contrary, we assume that the symbol E does not belong to any alphabet.
- ε -NFAs add a convenient feature but (in a sense) they bring us nothing new. They do not extend the class of languages that can be represented.
- Both NFAs and E-NFAs recognize exactly the same languages.
Epsilon (ε) - closure
Epsilon closure for a given state X is a set of states which can be reached from the states X with only (null) or E moves including the state X itself.
In other words, £-closure for a state can be obtained by union operation of the £-closure of the states which can be reached from X with a single E move in a recursive manner.
Example
Consider the following figure of NFA with ε move −
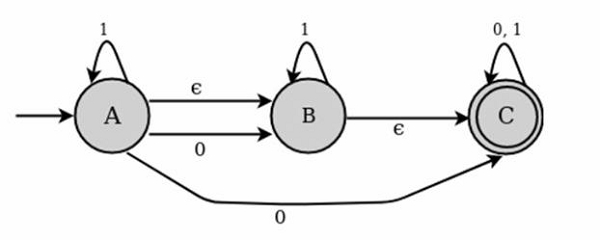
The transition state table for the above NFA is as follows −
| State | 0 | 1 | epsilon |
|---|---|---|---|
| A | B,C | A | B |
| B | - | B | C |
| C | C | C | - |
For the above example, ε closure are as follows −
- E closure( A) : {A, B,C}
- E closure( B) :{B,C}
- E closure( C) : {C}

