Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Dual Priority Queues
Existence of general methods to arrive at efficient DEPQ(Double Ended Priority Queue) data structures from single-ended priority queue (PQ) data structures that also provide an efficient implementation of the remove(bNode) operation (this operation eliminates the node bNode from the PQ). The simplest of these methods, dual structure method, maintains both a min PQ and a max PQ of all the DEPQ elements associated with correspondence pointers between the nodes of the min PQ and the max PQ that consist the same element.
Figure D displays a dual heap structure for the elements 7, 8, 3, 6, 5. Correspondence pointers are displayed as red arrows.
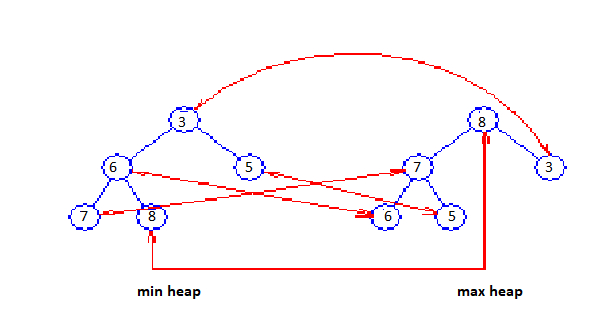
Figure D: Dual heap
Although the figure displays each element stored in both the min and the max heap, it is required to store each element in only one of the two heaps.
The isEmpty and size operations are applied by implementing a variable size that keeps track of the number of elements in the DEPQ. The minimum element is located at the root of the min heap and the maximum element is located at the root of the max heap. To insert an element B, we insert B into both the min and the max heaps and then set up correspondence pointers between the locations of B in the min and max heaps. To eliminate the minimum element, we do a removeMin from the min heap and a remove(bNode), where bNode is the corresponding node for the removed element, from the max heap. The maximum element is eliminated in an analogous way.
182 Views
