DSA using C - Recursion

Overview

Recursion refers to a technique in a programming language where a function calls itself. The function which calls itself is called a recursive method.

Characteristics

A recursive function must posses the following two characteristics.

  • Base Case(s)

  • Set of rules which leads to base case after reducing the cases.

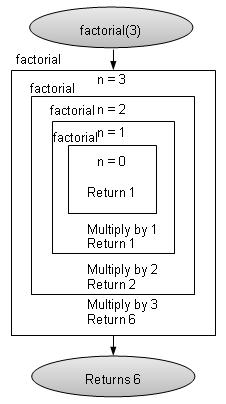
Recursive Factorial

Factorial is one of the classical example of recursion. Factorial is a non-negative number satisfying following conditions.

  • 0! = 1

  • 1! = 1

  • n! = n * n-1!

Factorial is represented by "!". Here Rule 1 and Rule 2 are base cases and Rule 3 are factorial rules.

As an example, 3! = 3 x 2 x 1 = 6

int factorial(int n){
   //base case
   if(n == 0){
      return 1;
   } else {
      return n * factorial(n-1);
   }
}
Factorial call trace

Recursive Fibonacci Series

Fibonacci Series is another classical example of recursion. Fibonacci series a series of integers satisfying following conditions.

  • F0 = 0

  • F1 = 1

  • Fn = Fn-1 + Fn-2

Fibonacci is represented by "F". Here Rule 1 and Rule 2 are base cases and Rule 3 are fibonnacci rules.

As an example, F5 = 0 1 1 2 3

Example

Live Demo 
#include <stdio.h>

int factorial(int n){
   //base case
   if(n == 0){
      return 1;
   } else {
      return n * factorial(n-1);
   }
}
int fibbonacci(int n){
   if(n ==0){
      return 0;
   }
   else if(n==1){
      return 1;
   } else {
      return (fibbonacci(n-1) + fibbonacci(n-2));
   }
}
main(){
   int n = 5;
   int i;
   printf("Factorial of %d: %d\n" , n , factorial(n));
   printf("Fibbonacci of %d: " , n);
   for(i=0;i<n;i++){
      printf("%d ",fibbonacci(i));            
   }
}

Output

If we compile and run the above program then it would produce following output −

Factorial of 5: 120
Fibbonacci of 5: 0 1 1 2 3
Advertisements