DSA using C - Graph

Previous
Quiz
Next

Overview

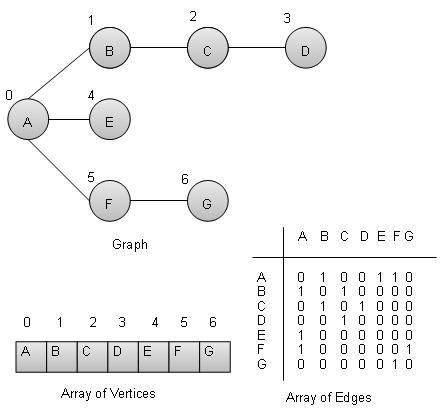
Graph is a datastructure to model the mathematical graphs. It consists of a set of connected pairs called edges of vertices. We can represent a graph using an array of vertices and a two dimentional array of edges.

Important terms

  • Vertex − Each node of the graph is represented as a vertex. In example given below, labeled circle represents vertices. So A to G are vertices. We can represent them using an array as shown in image below. Here A can be identified by index 0. B can be identified using index 1 and so on.

  • Edge − Edge represents a path between two vertices or a line between two vertices. In example given below, lines from A to B, B to C and so on represents edges. We can use a two dimentional array to represent array as shown in image below. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.

  • Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In example given below, B is adjacent to A, C is adjacent to B and so on.

  • Path − Path represents a sequence of edges between two vertices. In example given below, ABCD represents a path from A to D.

Graph

Basic Operations

Following are basic primary operations of a Graph which are following.

  • Add Vertex − add a vertex to a graph.

  • Add Edge − add an edge between two vertices of a graph.

  • Display Vertex − display a vertex of a graph.

Add Vertex Operation

//add vertex to the vertex list
void addVertex(char label){
struct vertex* vertex = 
   (struct vertex*) malloc(sizeof(struct vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}

Add Edge Operation

//add edge to edge array
void addEdge(int start,int end){
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}

Display Edge Operation

//display the vertex
void displayVertex(int vertexIndex){
   printf("%c ",lstVertices[vertexIndex]->label);
}

Traversal Algorithms

Following are important traversal algorithms on a Graph.

  • Depth First Search − traverses a graph in depthwards motion.

  • Breadth First Search − traverses a graph in breadthwards motion.

Depth First Search Algorithm

Depth First Search algorithm(DFS) traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search when a dead end occurs in any iteration.

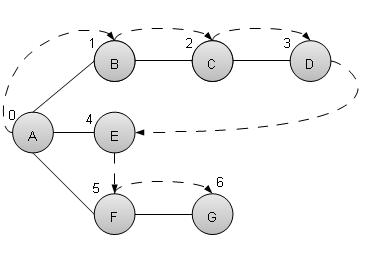
Depth First Search

As in example given above, DFS algorithm traverses from A to B to C to D first then to E, then to F and lastly to G. It employs following rules.

  • Rule 1 − Visit adjacent unvisited vertex. Mark it visited. Display it. Push it in a stack.

  • Rule 2 − If no adjacent vertex found, pop up a vertex from stack. (It will pop up all the vertices from the stack which do not have adjacent vertices.)

  • Rule 3 − Repeat Rule 1 and Rule 2 until stack is empty.

void depthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //push vertex index in stack
   push(0);

   while(!isStackEmpty()){
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      
      //no adjacent vertex found
      if(unvisitedVertex == -1){
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag        
   for(i=0;i < vertexCount;i++){
      lstVertices[i]->visited = false;
   }        
}

Breadth First Search Algorithm

Breadth First Search algorithm(BFS) traverses a graph in a breadthwards motion and uses a queue to remember to get the next vertex to start a search when a dead end occurs in any iteration.

Breadth First Search

As in example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs following rules.

  • Rule 1 − Visit adjacent unvisited vertex. Mark it visited. Display it. Insert it in a queue.

  • Rule 2 − If no adjacent vertex found, remove the first vertex from queue.

  • Rule 3 − Repeat Rule 1 and Rule 2 until queue is empty.

void breadthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //insert vertex index in queue
   insert(0);
   int unvisitedVertex;
   while(!isQueueEmpty()){
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();         
      
      //no adjacent vertex found
      while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
   } 
   //queue is empty, search is complete, reset the visited flag        
   for(i=0;i<vertexCount;i++){
      lstVertices[i]->visited = false;
   }    
}

Example

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 10

struct Vertex {
   char label;
   bool visited;
};

//stack variables
int stack[MAX]; 
int top=-1; 

//queue variables
int queue[MAX];
int rear=-1;
int front=0;
int queueItemCount = 0;

//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];

//adjacency matrix
int adjMatrix[MAX][MAX];

//vertex count
int vertexCount = 0;

//stack functions
void push(int item) { 
   stack[++top]=item; 
}
int pop() { 
   return stack[top--]; 
} 
int peek() {         
   return stack[top];
}
bool isStackEmpty(){
   return top == -1;
}
//queue functions
void insert(int data){
   queue[++rear] = data;
   queueItemCount++;
}
int removeData(){
   queueItemCount--;
   return queue[front++]; 
}
bool isQueueEmpty(){
   return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label){
   struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
   vertex->label = label;  
   vertex->visited = false;     
   lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end){
   adjMatrix[start][end] = 1;
   adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex){
   printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex){
   int i;
   for(i=0; i<vertexCount; i++)
      if(adjMatrix[vertexIndex][i]==1 && lstVertices[i]->visited==false)
         return i;
   return -1;
}
void depthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //push vertex index in stack
   push(0);

   while(!isStackEmpty()){
      //get the unvisited vertex of vertex which is at top of the stack
      int unvisitedVertex = getAdjUnvisitedVertex(peek());
      
      //no adjacent vertex found
      if(unvisitedVertex == -1){
         pop();
      } else {
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         push(unvisitedVertex);
      }
   }
   //stack is empty, search is complete, reset the visited flag        
   for(i=0;i < vertexCount;i++){
      lstVertices[i]->visited = false;
   }        
}
void breadthFirstSearch(){
   int i;
   //mark first node as visited
   lstVertices[0]->visited = true;
   
   //display the vertex
   displayVertex(0);   
   
   //insert vertex index in queue
   insert(0);
   int unvisitedVertex;
   while(!isQueueEmpty()){
      //get the unvisited vertex of vertex which is at front of the queue
      int tempVertex = removeData();         
      
      //no adjacent vertex found
      while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){    
         lstVertices[unvisitedVertex]->visited = true;
         displayVertex(unvisitedVertex);
         insert(unvisitedVertex);               
      }
   }
   //queue is empty, search is complete, reset the visited flag        
   for(i=0;i<vertexCount;i++){
      lstVertices[i]->visited = false;
   }    
}
main() {
   int i, j;
   
   for(i=0; i<MAX; i++) // set adjacency
      for(j=0; j<MAX; j++) // matrix to 0
         adjMatrix[i][j] = 0;

   addVertex('A');   //0
   addVertex('B');   //1
   addVertex('C');   //2
   addVertex('D');   //3
   addVertex('E');   //4
   addVertex('F');   //5
   addVertex('G');   //6

   /*      1  2  3   
   * 0  |--B--C--D
   * A--|
   * |
   * |     4 
   * |-----E
   * |     5  6
   * |  |--F--G
   * |--| 
   */        
   addEdge(0, 1);   //AB
   addEdge(1, 2);   //BC
   addEdge(2, 3);   //CD
   addEdge(0, 4);   //AC
   addEdge(0, 5);   //AF
   addEdge(5, 6);   //FG
   printf("Depth First Search: ");
   
   //A B C D E F G
   depthFirstSearch();              
   printf("\nBreadth First Search: ");
   
   //A B E F C G D
   breadthFirstSearch();
}

If we compile and run the above program then it would produce following result −

Depth First Search: A B C D E F G 
Breadth First Search: A B E F C G D
Print Page
Previous
Next
Advertisements